Alla fine mi è venuta una domanda che ha mandato fuori strada il generatore di Wichman-Hill. Non è così naturale come si potrebbe desiderare, ma spero che sia abbastanza spettacolare.

Ecco il problema: studia la distribuzione di $$ X = -10U_1 - 22U_2 + 38U_3 - 3U_4 + U_5 + 4U_6 - 38 U_7 $$ con l'uniforme $ U_i $ iid su $ (0,1) $.

Disegneremo solo un istogramma.

  x <- c (-10, -22, 38, -3, 1, 4, -38) RNGkind (kind = "Mersenne") U <- matrice (runif (7 * 1e6), nrow = 7) hist (colSums (x * U), break = seq (-70,50, by = 0.25), col = "black")  

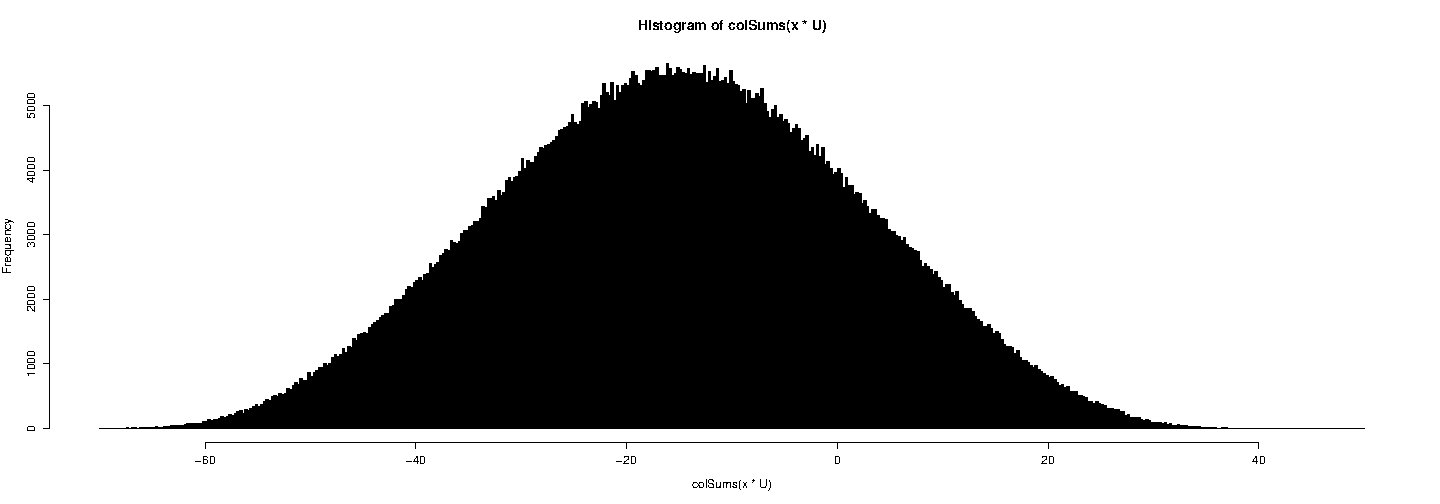
Ora prova con Wichman-Hill:

  RNGkind (kind = "Wichman") U <- matrix (runif (7 * 1e6), nrow = 7) hist (colSums (x * U), breaks = seq (-70,50, by = 0.25), col = "black")  

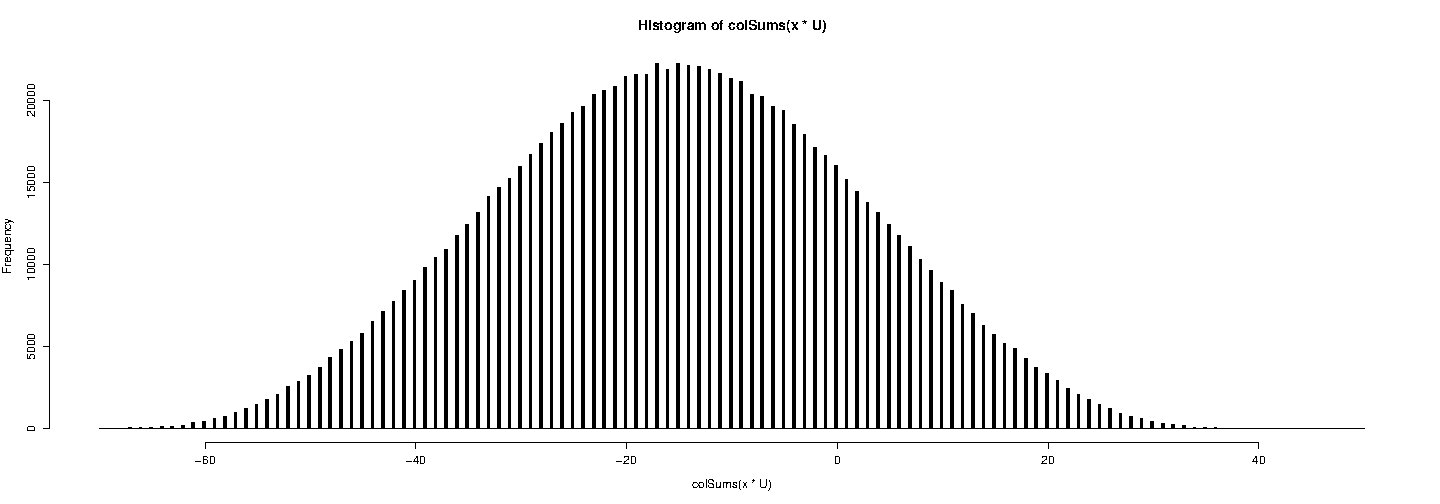
Sì, tutti i valori generati sono interi:

  > head (colonne (x * U), 20) [1] 3-9-52-21-23-14-18 8-23 12 5 4-17-16-19-44 5 4-23 [20] -15  

Se alcune persone mostrano interesse, posso spiegare brevemente come ho costruito questo esempio.

Ecco uno schizzo del costruzione dell'esempio. I generatori congruenziali lineari si basano su una sequenza in $ [1, \ dots m-1] $ definita da $ x_ {n + 1} = \ alpha x_n \ [m] $ (che significa modulo $ m $), con $ \ gcd (\ alpha, m) = 1 $. I numeri pseudo casuali $ u_n = {1 \ over m} x_n $ si comportano all'incirca come numeri casuali uniformi in $ (0,1) $.

Un problema noto di questi generatori è che puoi trovare molti coefficienti $ a_0, a_1, \ dots, a_k \ in \ mathbb {Z} $ tali che $$ a_0 + a_1 \ alpha + \ cdots + a_k \ alpha ^ k = 0 \ [m]. $$ Ciò risulta in $ a_0 x_n + \ cdots + a_k x_ {n + k} = 0 \ [m] $ per tutti $ n $, che a sua volta si traduce in $ a_0 u_n + \ cdots + a_k u_ {n + k} \ in \ mathbb {Z } $. Ciò significa che tutte le $ (k + 1) $ - tuple $ (u_n, \ dots, u_ {n + k}) $ cadono in piani ortogonali a $ (a_0, \ dots, a_k) '$.

Ovviamente con $ k = 1 $, $ a_0 = \ alpha $ e $ a_1 = -1 $, hai un esempio del genere. Ma poiché $ \ alpha $ è solitamente grande, questo non darà un bell'esempio come sopra. Il punto è trovare valori "piccoli" $ a_0, \ dots, a_k $.

Siano $$ L = \ {(a_0, \ dots, a_k) \: \ a_0 + a_1 \ alpha + \ cdots + a_k \ alpha ^ k = 0 \ [m] \}. $$ Questo è un $ \ mathbb {Z} $ - reticolo.

Usando un po 'di algebra modulare, si può controllare che $ f_0 = (m, 0, \ dots, 0)' $, $ f_1 = (\ alpha, -1,0, \ dots, 0) '$, $ f_2 = (0, \ alpha, -1,0, \ dots, 0)' $, $ \ dots $, $ f_k = (0, \ dots, 0, \ alpha, -1) '$ è una base di questo reticolo (questo è il risultato chiave qui ...).

Il problema è quindi trovare un vettore breve in $ L $. Ho usato algoritmo LLL per questo scopo. L'algoritmo 2.3 di Brian Ripley Stochastic Simulation indicato (dopo la mia risposta) da kjetil b halvorsen avrebbe potuto essere usato.

Per Wichman-Hill, il Teorema cinese dei resti permette di verificare facilmente che sia equivalente a un generatore del tipo sopra, con $ \ alpha = 16555425264690 $ e $ m = 30269 \ times30307 \ times30323 = 27817185604309 $.

L'applicazione più interessata a piccole deviazioni dalla correlazione è la crittografia. La capacità di prevedere un valore pseudo-casuale con una precisione migliore del normale può tradursi in capacità superiori per rompere gli schemi di crittografia.

Questo può essere illustrato con un esempio alquanto artificiale progettato per aiutare l'intuizione. Mostra come un cambiamento veramente radicale nella prevedibilità può essere sostenuto da una correlazione seriale arbitrariamente piccola. Siano $ X_1, X_2, \ ldots, X_n $ le variabili normali standard. Sia $ \ bar X = (X_1 + X_2 + \ cdots + X_n) / n $ la loro media e designiamo

$$ Y_i = X_i - \ bar X $$

come loro residui. È elementare stabilire che (1) $ Y_i $ hanno distribuzioni Normali identiche ma (2) la correlazione tra $ Y_i $ e $ Y_j $ (per $ i \ ne j $) è $ -1 / (n-1) $. Per $ n $ grandi questo è trascurabile, giusto?

Considera il compito di prevedere $ Y_n $ da $ Y_1, Y_2, \ ldots, Y_ {n-1} $. Nell'ipotesi di indipendenza, il miglior predittore possibile è la loro media. In realtà, però, la costruzione di $ Y_i $ garantisce che la loro somma sia zero, da cui

$$ \ hat {Y_n} = - \ sum_ {i = 1} ^ {n-1} Y_i $$

è un predittore perfetto (privo di errori) di $ Y_n $. Questo mostra come anche un minimo di correlazione possa migliorare enormemente la prevedibilità. Nella crittoanalisi i dettagli saranno diversi - si studiano i flussi di bit, non le variabili normali, e le correlazioni seriali possono essere davvero minime - ma il potenziale per risultati altrettanto drammatici esiste comunque.

Per quelli a chi piace giocare con le cose, la seguente simulazione in R replica questa situazione ipotetica e riassume la media e le deviazioni standard degli errori di previsione. Riassume anche i coefficienti di correlazione seriale del primo ordine del $ Y_i $ simulato. Per riferimento, fa lo stesso per $ X_i $.

  predicono.mean <- funzione (x) mean (x [-length (x )])
predire.correl <- funzione (x) -sum (x [-lunghezza (x)]) n <- 1e5set.seed (17) sim <- replicate (1e3, {x <-rnorm (n) y <- x - media (x) c (predire.meano (y) - y [n], predire.correl (y) - y [n], predire.mean (x) - x [n], predire.correl (x) - x [n], cor (y [-1], y [-n]))}) rownames (sim) <- c ("Mean method", "Exploit", "Mean (reference)", "Exploit (reference) "," Autocorrelation ") zapsmall (apply (sim, 1, mean)) zapsmall (apply (sim, 1, sd))  

Come scritto, ci vorrà una buona frazione di a minuto da eseguire: esegue $ 1000 $ simulazioni del caso $ n = 10 ^ 5 $. La tempistica è proporzionale al prodotto di questi numeri, quindi ridurlo di un ordine di grandezza darà una svolta soddisfacente per gli esperimenti interattivi. In questo caso, poiché è stato eseguito un numero così elevato di simulazioni, i risultati saranno abbastanza accurati e sono

  Metodo medio Exploit Mean (riferimento) Exploit (riferimento) Autocorrelazione -0.064697 0.000000 - 0.064697 5.502087 -0.000046 Metodo della media Exploit Mean (riferimento) Exploit (riferimento) Autocorrelation 1.0235 0.0000 1.0235 321.8314 0.0031 

In media, la stima di $ Y_n $ con la media dei valori precedenti ha commesso un errore di $ -0,06 $, ma la deviazione standard di questi errori era vicina a $ 1 $. L'exploit offerto dal riconoscimento della correlazione è stato assolutamente perfetto: ha sempre ottenuto la previsione corretta. Tuttavia, quando applicato ai valori veramente indipendenti $ (X_i) $, l'exploit si è comportato in modo terribile, con una deviazione standard di $ 321,8 $ (essenzialmente uguale a $ \ sqrt {n} $). Questo compromesso tra presupposti e prestazioni è istruttivo!