Definire $ F (n, k) $ come il numero di modi per allocare $ k $ opzioni a $ n $ flip in modo che ogni opzione appaia 0 o $ \ geq 2 $ volte. Quindi la probabilità che tu veda esattamente $ y $ valori univoci quando tiri un $ k $ dadi $ n $ volte è:

$$ Pr (Y = y) = \ frac {{k \ scegli y} {n \ scegli y} y! F (ny, ky)} {k ^ n} $$

Fondamentalmente, ci sono $ {k \ scegli y} $ modi per selezionare $ y $ opzioni uniche da tutte le opzioni $ k $, $ {n \ scegli y} $ modi per selezionare i $ y $ rotoli per queste opzioni uniche e $ y! $ ordinamenti delle opzioni $ y $ all'interno di questi rotoli.

Non resta che calcolare $ F (n, k) $. Ci sono alcuni semplici casi e poi una definizione ricorsiva:

\ begin {align *} F (0, k) & = 1 & \ forall ~ k \ geq 0 \\ F (1, k) & = 0 & \ forall ~ k \ geq 0 \\ F (n, 0) & = 0 & \ forall ~ n \ geq 1 \\ F (n, k) & = F (n, k-1) + \ sum_ {i = 2} ^ n {n \ scegli i} F (ni, k-1) & \ forall ~ n \ geq 2, k \ geq 1 \ end {align *}

Il ricorsivo step seleziona un'opzione arbitraria e considera separatamente il numero di allocazioni per le quali appare $ 0, 2, 3, \ ldots, n $ volte. Questa formulazione consente il calcolo dell'intero pmf in $ O (n ^ 2k) $ runtime, che dovrebbe essere molto più efficiente della somma di tutte le partizioni valide della distribuzione multinomiale. Ecco un'implementazione R:

  uniquePMF <- function (n, k) {F <- matrix (0, nrow = n + 1, ncol = k + 1) F [1,] <- 1 per (.k in 1: k) {per (.n in 2: n) {F [.n + 1, .k + 1] <- F [.n + 1, .k] + sum (scegli (.n, 2: .n) * F [.n- (2: .n) + 1, .k])}} out <- sapply (0: min (n , k), funzione (y) scegli (k, y) * scegli (n, y) * fattoriale (y) * F [n-y + 1, k-y + 1]) / k ^ n nomi (fuori) <- 0: min (n, k) out}  

Questo restituisce i risultati calcolati a mano per il caso $ n = 2, k = 3 $:

  uniquePMF (2, 3) # 0 1 2
# 0.3333333 0.0000000 0.6666667  

Può anche gestire comodamente istanze più grandi (qui $ n = k = 100 $):

  plot (0: 100, uniquePMF (100, 100), xlab = "y", ylab = "Pr (Y = y)")  

Esiste una soluzione $ O (n) $ efficiente e semplice.

Espandendo il polinomio

$$ f_ {n, r } = \ left (x_1 + x_2 + \ cdots + x_r \ right) ^ n = \ sum_ {i_1, i_2, \ ldots, i_r} \ binom {n} {i_1, i_2, \ ldots, i_r} x_1 ^ {i_1} x_2 ^ {i_2} \ cdots x_r ^ {i_r}, $$

per ciascuno dei $ \ binom {r} {y} $ sottoinsiemi di $ y $ delle variabili ci sarà un termine come questo

$$ \ binom {n} {1,1, \ ldots, 1, i_ {y + 1}, \ ldots, i_r} \ left (x_1x_2 \ cdots x_y \ x_ {y + 1} ^ {i_ {y + 1}} \ cdots x_r ^ {i_r} \ right) $$

il cui coefficiente fornisce il numero di volte almeno $ y $ di le variabili vengono visualizzate solo una volta. Questo coefficiente può essere trovato differenziando $ f_ {n, r} $ rispetto a ciascuna di quelle $ y $ variabili, impostando i valori di queste variabili a $ 0 $ e impostando i valori delle rimanenti $ ry $ variabili a $ 1 $ , perché

$$ \ frac {\ partial ^ y} {\ partial x_1 \ partial x_2 \ cdots \ partial x_y} \ left (x_1x_2 \ cdots x_y \ x_ {y + 1} ^ {i_ { y + 1}} \ cdots x_r ^ {i_r} \ right) = x_ {y + 1} ^ {i_ {y + 1}} \ cdots x_r ^ {i_r} $$

restituisce $ 1 $ e tutti gli altri termini hanno almeno una delle prime variabili $ y $ come fattore, da cui valutano $ 0 $.

Calcolo di questa derivata per l'espressione originale di $ f_ {n, r} $ produce (utilizzando la notazione fattoriale decrescente per il coefficiente)

$$ \ eqalign {& \ frac {\ partial ^ y} {\ partial x_1 \ partial x_2 \ cdots \ partial x_y} \ sinistra (x_1 + x_2 + \ cdots + x_r \ destra) ^ n \\ & = n (n-1) \ cdots (n-y + 1) \ sinistra (x_1 + x_2 + \ cdots + x_r \ destra) ^ {ny} \\ & = n _ {(y)} \ left (x_1 + x_2 + \ cdots + x_r \ right) ^ {ny}.} $$

Quando $ y $ di $ x_i $ è uguale a $ 0 $ e il restante $ ry $ uguale $ 1 $, il lato destro restituisce

$$ n _ {(y)} (ry) ^ {ny}. $$

Moltiplicando per $ \ binom {r } {y} $ per tenere conto di tutte le possibili combinazioni di variabili $ y $ e l'applicazione del Principio di esclusione dall'inclusione ("PIE") produce il numero di volte in cui le variabili $ y $ appaiono esattamente una volta, che è

$$ \ binom {r} {y} \ sum_ {j = y} ^ {\ min (r, n)} (-1) ^ {jy} ( rj) ^ {nj} n _ {(j)} \ binom {ry} {jy}. $$

Dividendolo per $ r ^ n $ si ottengono le probabilità associate. Lo sforzo di calcolo è $ O (\ min (r, n) -y) $.

Niente è gratis! Come nella maggior parte delle applicazioni della Torta, questa è una somma alternata di termini che possono variare radicalmente in dimensioni, con il risultato finale molto più piccolo dei termini più grandi. Può esserci una perdita catastrofica di precisione, quindi è necessaria un'aritmetica ad alta precisione (o, meglio ancora, razionale esatto). Con quello disponibile, l'implementazione è notevolmente breve. Eccolo in Mathematica:

  p [n_, k_]: = n ^ k; p [n_, 0]: = 1; f [n_, d_, k_]: = Binomiale [d, k] Somma [(- 1) ^ (jk) Binomiale [dk, jk] Fattoriale [n, j] p [ dj, nj], {j, k, Min [d, n]}]  

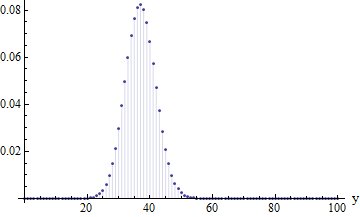
Come esempio, tracciamo la distribuzione completa per un particolare $ n $ e $ r $:

  Con [{n = 100, r = 100}, DiscretePlot [f [n, r, y] / r ^ n, {y, 0, Min [n, r]}]] 

Come esempio, si consideri il caso $ n = 4 $, $ r = 3 $, e valori di $ y $ da $ 0 $ a $ 3 $. L'espansione di $ f_ {4,3} $ è

$$ x_1 ^ 4 + x_2 ^ 4 + x_3 ^ 4 \\\ color {blue} {+ 4 x_2 x_1 ^ 3 + 4 x_3 x_1 ^ 3 + 4 x_1 x_2 ^ 3 + 4 x_3x_2 ^ 3 + 4 x_1 x_3 ^ 3 + 4 x_2x_3 ^ 3} \\ + 6 x_2 ^ 2 x_1 ^ 2 + 6 x_2 ^ 2 x_3 ^ 2 + 6 x_3 ^ 2 x_1 ^ 2 \\\ colore {rosso} {+ 12 x_1 x_2 x_3 ^ 2 +12 x_1 x_2 ^ 2 x_3 +12 x_1 ^ 2 x_2 x_3}. $$

Considera il calcolo per $ y = 1 $ .

• I termini contenenti esattamente un $ x_1 $ sono

  $$ \ color {blue} {4 x_1 x_2 ^ 3 + 4 x_1 x_3 ^ 3} + \ color {red} {12 x_1 x_2 x_3 ^ 2 +12 x_1 x_2 ^ 2 x_3}. $$

  La somma di questi coefficienti è $ 4 + 4 + 12 + 12 = 32 $. Quindi stimeremmo che il numero totale di termini con uno solo di $ x_i $ sarebbe $ 3 \ times 32 = 96 $.

• Non abbiamo ancora finito. I termini contenenti un $ x_1 $ e un altro $ x_i $ sono

  $$ \ color {red} {12 x_1 x_2 x_3 ^ 2 + 12 x_1 x_2 ^ 2 x_3}. $$

  Questo ci dice che quando abbiamo contato i termini $ x_1 $ in precedenza, abbiamo sovrastimato di $ 12 + 12 = 24 $. Il conteggio totale quindi è $ 3 \ volte 24 = 72 $.

• Ora abbiamo finito, perché non sono possibili termini con esattamente un'istanza di tre lati.

Di conseguenza, il count for $ y = 1 $ è

$$ 96 - 72 + 0 = 24. $$

In effetti, questa è la somma dei coefficienti di

$ $ \ color {blu} {4 x_2 x_1 ^ 3 + 4 x_3 x_1 ^ 3 + 4 x_1 x_2 ^ 3 + 4 x_3x_2 ^ 3 + 4 x_1 x_3 ^ 3 + 4 x_2x_3 ^ 3}. $$

Questo è fondamentalmente un problema generalizzato di raccolta di coupon. Non credo che troverai una soluzione facile in forma chiusa. In generale, la distribuzione dei lanci dei dadi è multinomiale:

$$ \ binom {n} {a_1, a_2, \ cdots, a_r} (1 / r) ^ n, $$

dove $ a_i $ rappresenta il numero di volte in cui $ i $ viene lanciato e $ a_1 + \ cdots + a_r = n $. Allora la risposta è:

$$ (1 / r) ^ n \ sum \ binom {n} {a_1, a_2, \ cdots, a_r}, $$

dove il la somma è su tutte le combinazioni di $ a_i $ tali che esattamente $ y $ di esse siano diverse da zero. I.E. stai guardando tutte le partizioni di $ n = a_1 + \ cdots + a_r $ in modo tale che esattamente $ y $ siano diversi da zero. Puoi usare un po 'di simmetria per semplificare ulteriormente tutto sommando tutte le combinazioni di $ n = a_1 + \ cdots + a_y $ con $ a_i>0 $ per $ i = 1,2, \ cdots, y $ e $ a_i = 0 $ per $ i>y $, e quindi tenendo conto della loro molteplicità tramite $ \ binom {n} {a_1} \ binom {n-a_1} {a_2} \ cdots $.