Ci sono diversi punti che puoi migliorare nel codice
Condizioni al contorno errate
Il tuo modello è fissato su I = 1 per il tempo zero. Puoi modificare questo punto nel valore osservato o aggiungere un parametro nel modello che sposta l'ora di conseguenza.
init <- c (S = N-1, I = 1, R = 0)
# dovrebbe essere
init <- c (S = N-Infected [1], I = Infected [1], R = 0)
Scale di parametri disuguali
Come altre persone hanno notato l'equazione
$$ I '= \ beta \ cdot S \ cdot I - \ gamma \ cdot I $$
ha un valore molto grande per $ S \ cdot I $ questo fa sì che il valore del parametro $ \ beta $ molto piccolo e l'algoritmo che controlla se le dimensioni dei passaggi nelle iterazioni raggiungono un certo punto non varierà i passaggi in $ \ beta $ e $ \ gamma $ allo stesso modo (le modifiche in $ \ beta $ avranno un effetto molto maggiore rispetto alle modifiche in $ \ gamma $ ).
Puoi cambiare la scala nella chiamata alla funzione optim per correggere queste differenze di dimensione (e controllare la tela di iuta ti permette di vedere se funziona un po '). Ciò viene fatto utilizzando un parametro di controllo. Inoltre potresti voler risolvere la funzione in fasi separate rendendo l'ottimizzazione dei due parametri indipendente l'una dall'altra (vedi di più qui: Come gestire le stime instabili durante l'adattamento della curva? questo viene fatto anche in il codice qui sotto, e il risultato è una convergenza molto migliore; sebbene si raggiungano comunque i limiti dei limiti inferiore e superiore)
Opt <- optim (c (2 * coefficients (mod) [2] / N, coefficients (mod) [2]), RSS.SIR, method = "L-BFGS-B", inferiore = inferiore, superiore = superiore,
hessian = TRUE, control = list (parscale = c (1 / N, 1), factr = 1))
più intuitivo potrebbe essere scalare il parametro nella funzione (nota il termine beta / N al posto di beta )
SIR <- funzione (ora, stato, parametri) {
par <- as.list (c (stato, parametri))
con (par, {dS <- -beta / N * S * I
dI <- beta / N * S * I - gamma * I
dR <- gamma * I
elenco (c (dS, dI, dR))
})
}
Condizione iniziale
Perché il valore di $ S $ è all'inizio più o meno costante (ovvero $ S \ approx N $ ) l'espressione per gli infetti all'inizio può essere risolta come un'unica equazione:
$$ I '\ approx (\ beta \ cdot N - \ gamma) \ cdot I $$
Quindi puoi trovare una condizione iniziale utilizzando un adattamento esponenziale iniziale:
# ottiene una buona condizione di partenza
mod <- nls (Infected ~ a * exp (b * day),
start = list (a = Infected [1],
b = log (infetto [2] / infetto [1])))
Instabile, correlazione tra $ \ beta $ e $ \ gamma $
C'è un po 'di ambiguità su come scegliere $ \ beta $ e $ \ gamma $ per la condizione di partenza.
Ciò renderà anche il risultato della tua analisi non così stabile. L'errore nei singoli parametri $ \ beta $ e $ \ gamma $ sarà molto grande perché molte coppie di $ \ beta $ e $ \ gamma $ fornirà un RSS più o meno altrettanto basso.
Il grafico seguente è per la soluzione $ \ beta = 0.8310849; \ gamma = 0,4137507 $
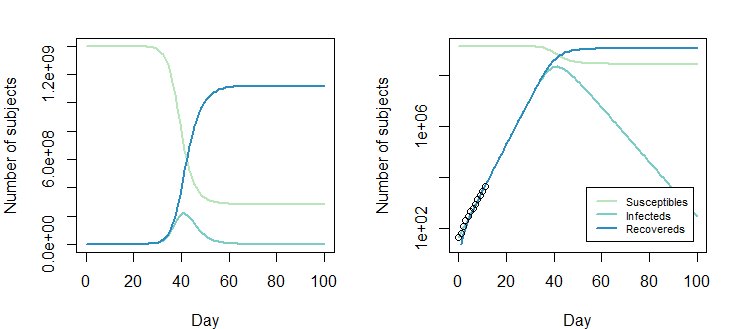
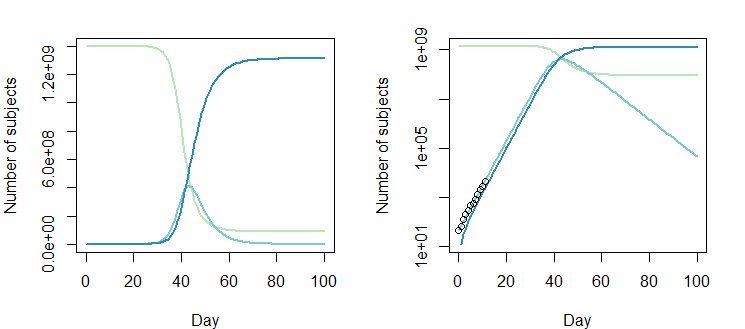
Tuttavia, il valore Opt_par modificato $ \ beta = 0.8310849-0.2; \ gamma = 0.4137507-0.2 $ funziona altrettanto bene:
Utilizzo di una parametrizzazione diversa
La funzione optim ti permette di leggere l'iuta
> Opt <- optim (optimsstart, RSS.SIR, method = "L-BFGS-B", lower = lower, upper = upper,
+ iuta = VERO)
> Opt $ hessian
b
b 7371274104-7371294772
-7371294772 7371315619
La hessiana può essere correlata alla varianza dei parametri ( In R, dato un output da optim con una matrice hessiana, come calcolare gli intervalli di confidenza dei parametri usando la matrice hessiana?). Ma nota che per questo scopo hai bisogno dell'Hessian della probabilità di log che non è lo stesso dell'RSS (differisce di un fattore, vedi il codice sotto).
Sulla base di ciò puoi vedere che la stima della varianza campionaria dei parametri è molto ampia (il che significa che i tuoi risultati / stime non sono molto accurati). Ma nota anche che l'errore è molto correlato. Ciò significa che è possibile modificare i parametri in modo tale che il risultato non sia molto correlato. Alcuni esempi di parametrizzazione potrebbero essere:
$$ \ begin {array} {}
c & = & \ beta - \ gamma \\
R_0 & = & \ frac {\ beta} {\ gamma}
\ end {array} $$
tale che le vecchie equazioni (si noti che viene utilizzato un ridimensionamento di 1 / N):
$$ \ begin {array} {rccl}
S ^ \ prime & = & - \ beta \ frac {S} {N} & I \\
I ^ \ prime & = & (\ beta \ frac {S} {N} - \ gamma) & I \\
R ^ \ prime & = & \ gamma &I
\ end {array}
$$
diventa
$$ \ begin {array} {rccl}
S ^ \ prime & = & -c \ frac {R_0} {R_0-1} \ frac {S} {N} & I& \\
I ^ \ prime & = & c \ frac {(S / N) R_0 - 1} {R_0-1} &I& \ underbrace {\ approx c I} _ {\ text {for $ t = 0 $ quando $ S / N \ circa 1 $}} \\
R ^ \ prime & = & c \ frac {1} {R_0-1} & I&
\ end {array}
$$
che è particolarmente interessante poiché ottieni questo $ I ^ \ prime = cI $ approssimativo per l'inizio. TQuesto ti farà vedere che stai sostanzialmente stimando la prima parte che è approssimativamente una crescita esponenziale. Sarai in grado di determinare con estrema precisione il parametro di crescita, $ c = \ beta - \ gamma $ . Tuttavia, $ \ beta $ e $ \ gamma $ o $ R_0 $ , non può essere facilmente determinato.
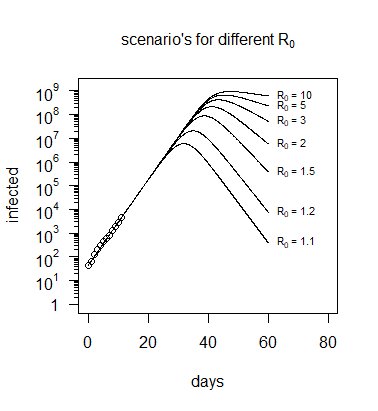
Nel codice seguente viene eseguita una simulazione con lo stesso valore $ c = \ beta - \ gamma $ ma con valori diversi per $ R_0 = \ beta / \ gamma $ . Puoi vedere che i dati non sono in grado di permetterci di differenziare quale scenario diverso (quale diverso $ R_0 $ ) abbiamo a che fare (e avremmo bisogno di più informazioni, ad es le posizioni di ogni individuo infetto e cercando di vedere come si è diffusa l'infezione).
È interessante che diversi articoli fingano già di avere stime ragionevoli di $ R_0 $ . Ad esempio questo preprint Novel coronavirus 2019-nCoV: stima anticipata dei parametri epidemiologici e previsioni epidemiche ( https://doi.org/10.1101/2020.01.23.20018549)
Un po 'di codice:
####
####
####
libreria (deSolve)
libreria (RColorBrewer)
#https: //en.wikipedia.org/wiki/Timeline_of_the_2019%E2%80%9320_Wuhan_coronavirus_outbreak#Cases_Chronology_in_Mainland_China
< infetto- c (45, 62, 121, 198, 291, 440, 571, 830, 1287, 1975, 2744, 4515)
giorno <- 0: (length (Infected) -1)
N <- 1400000000 #pop della Cina
### modifica 1: usa una diversa condizione al contorno
### init <- c (S = N-1, I = 1, R = 0)
init <- c (S = N-Infected [1], I = Infected [1], R = 0)
trama (giorno, infetto)
SIR <- funzione (ora, stato, parametri) {
par <- as.list (c (stato, parametri))
#### modifica 2; utilizzare variabili ugualmente scalate
con (par, {dS <- -beta * (S / N) * I
dI <- beta * (S / N) * I - gamma * I
dR <- gamma * I
elenco (c (dS, dI, dR))
})
}
SIR2 <- funzione (ora, stato, parametri) {
par <- as.list (c (stato, parametri))
####
#### utilizzare come variabile di modifica delle variabili
#### const = (beta-gamma)
#### delta = gamma / beta
#### R0 = beta / gamma > 1
####
#### beta-gamma = beta * (1-delta)
#### beta-gamma = beta * (1-1 / R0)
#### gamma = beta / R0
con (par, {
beta <- const / (1-1 / R0)
gamma <- const / (R0-1)
dS <- - (beta * (S / N)) * I
dI <- (beta * (S / N) -gamma) * I
dR <- (gamma) * I
elenco (c (dS, dI, dR))
})
}
RSS.SIR2 <- funzione (parametri) {
nomi (parametri) <- c ("const", "R0")
out <- ode (y = init, times = day, func = SIR2, parms = parameters)
adatta <- out [, 3]
RSS <- sum ((Infected - fit) ^ 2)
ritorno (RSS)
}
### tracciare valori diversi R0
# usa il modello esponenziale ordinario per determinare const = beta - gamma
const <- coef (mod) [2]
RSS.SIR <- funzione (parametri) {
nomi (parametri) <- c ("beta", "gamma")
out <- ode (y = init, times = day, func = SIR, parms = parameters)
adatta <- out [, 3]
RSS <- sum ((Infected - fit) ^ 2)
ritorno (RSS)
}
inferiore = c (0, 0)
superiore = c (1, 1) ### regola il limite perché scala 1 / N diversa
### modifica: ottieni una buona condizione di partenza
mod <- nls (Infected ~ a * exp (b * day),
start = list (a = Infected [1],
b = log (infetto [2] / infetto [1])))
optimsstart <- c (2,1) * coef (mod) [2]
set.seed (12)
Opt <- optim (optimsstart, RSS.SIR, method = "L-BFGS-B", lower = lower, upper = upper,
iuta = VERO)
Optare
### matrice di covarianza stimata dei coefficienti
### nota il grande errore, ma anche la forte correlazione (quasi 1)
## nota il ridimensionamento con stima di sigma perché dobbiamo usare l'Assia di loglikelihood
sigest <- sqrt (Opt $ value / (length (Infected) -1))
risolvere (1 / (2 * sigest ^ 2) * Opt $ hessian)
####
#### utilizzando parametri alternativi
#### per questo usiamo la funzione SIR2
####
optimsstart <- c (coef (mod) [2], 5)
inferiore = c (0, 1)
upper = c (1, 10 ^ 3) ### regola il limite perché ora usiamo R0 che dovrebbe essere >1
set.seed (12)
Opt2 <- optim (optimsstart, RSS.SIR2, method = "L-BFGS-B", inferiore = inferiore, superiore = superiore,
hessian = TRUE, control = list (maxit = 1000,
parscale = c (10 ^ -3,1)))
Opt2
# ora la varianza stimata del primo parametro è piccola
# il 2 ° parametro è ancora con grande varianza
#
# quindi possiamo prevedere molto bene il beta-gamma
# questa beta - gamma è il coefficiente di crescita iniziale
# ma i valori individuali di beta e gamma non sono molto noti
#
# si noti inoltre che l'iuta non è al MLE poiché abbiamo raggiunto il limite inferiore
#
sigest <- sqrt (Opt2 $ value / (length (Infected) -1))
risolvere (1 / (2 * sigest ^ 2) * Opt2 $ hessian)
#### Possiamo anche stimare la varianza di
#### Stima Monte Carlo
##
## supponendo che i dati vengano distribuiti come media +/- q media
## con q tale che significa RSS = 52030
##
##
##
### Due funzioni RSS per eseguire l'ottimizzazione in modo annidato
RSS.SIRMC2 <- funzione (const, R0) {
parametri <- c (const = const, R0 = R0)
out <- ode (y = init, times = day, func = SIR2, parms = parameters)
adatta <- out [, 3]
RSS <- sum ((Infected_MC - fit) ^ 2)
ritorno (RSS)
}
RSS.SIRMC <- funzione (const) {
ottimizzare (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = const) $ obiettivo
}
getOptim <- function () {
opt1 <- ottimizza (RSS.SIRMC, inferiore = 0, superiore = 1)
opt2 <- ottimizza (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = opt1 $ minimo)
return (elenco (RSS = opt2 $ obiettivo, const = opt1 $ minimo, R0 = opt2 $ minimo))
}
# dati modellati che utilizziamo per generare ripetutamente dati con rumore
Opt_par <- Opt2 $ par
nomi (Opt_par) <- c ("const", "R0")
modInfected <- data.frame (ode (y = init, times = day, func = SIR2, parms = Opt_par)) $ I
# facendo il modello annidato per ottenere RSS
set.seed (1)
Infected_MC <- Infected
modnested <- getOptim ()
errrate <- modnested $ RSS / sum (infetto)
par <- c (0,0)
per (i in 1: 100) {
Infected_MC <- rnorm (length (modInfected), modInfected, (modInfected * errrate) ^ 0.5)
OptMC <- getOptim ()
par <- rbind (par, c (OptMC $ const, OptMC $ R0))
}
par <- par [-1,]
trama (par, xlab = "const", ylab = "R0", ylim = c (1,1))
titolo ("Simulazione Monte Carlo")
cov (par)
### conclusione: il parametro R0 non può essere stimato in modo affidabile
##### Fine della stima Monte Carlo
### tracciare valori diversi R0
# usa il modello esponenziale ordinario per determinare const = beta - gamma
const <- coef (mod) [2]
R0 <- 1.1
# grafico
grafico (-100, -100, xlim = c (0,80), ylim = c (1, N), log = "y",
ylab = "infetto", xlab = "giorni", yaxt = "n")
asse (2, las = 2, at = 10 ^ c (0: 9),
etichette = c (espressione (1),
espressione (10 ^ 1),
espressione (10 ^ 2),
espressione (10 ^ 3),
espressione (10 ^ 4),
espressione (10 ^ 5),
espressione (10 ^ 6),
espressione (10 ^ 7),
espressione (10 ^ 8),
espressione (10 ^ 9)))
axis (2, at = rep (c (2: 9), 9) * rep (10 ^ c (0: 8), each = 8), labels = rep ("", 8 * 9), tck = -0.02 )
title (bquote (paste ("scenario's for different", R [0])), cex.main = 1)
# tempo
t <- seq (0,60,0.1)
# modello di trama con differenti R0
per (R0 in c (1.1,1.2,1.5,2,3,5,10)) {
fit <- data.frame (ode (y = init, times = t, func = SIR2, parms = c (const, R0))) $ I
linee (t, fit)
testo (t [601], adatta [601],
bquote (incolla (R [0], "=",. (R0))),
cex = 0,7, pos = 4)
}
# osservazioni sulla trama
punti (giorno, infetto)
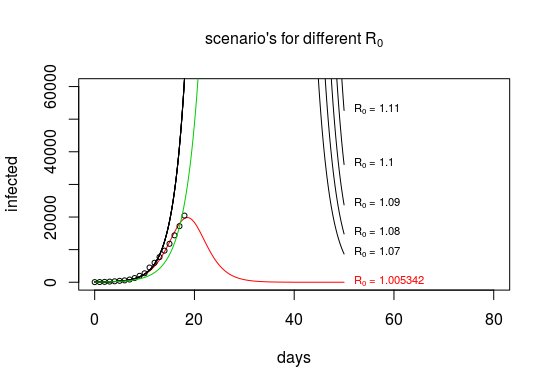
Come viene stimato R0?
Il grafico sopra (che viene ripetuto sotto) ha mostrato che non c'è molta variazione nel numero di "infetti" in funzione di $ R_0 $ e i dati sul numero di persone infette non forniscono molte informazioni su $ R_0 $ (tranne se è superiore o inferiore a zero).
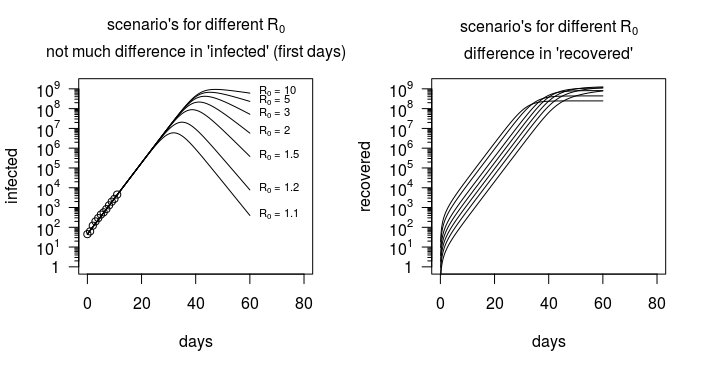
Tuttavia, per il modello SIR esiste una grande variazione nel numero di ripristinati o nel rapporto infetti / ripristinati. Questo è mostrato nell'immagine sottostante dove il modello è tracciato non solo per il numero di persone infette ma anche per il numero di persone guarite. Sono tali informazioni (oltre a dati aggiuntivi come informazioni dettagliate su dove e quando le persone sono state infettate e con chi hanno avuto contatti) che consentono la stima di $ R_0 $ .
Aggiorna
Nell'articolo del tuo blog scrivi che l'adattamento sta portando a un valore di $ R_0 \ approx 2 $ .
Tuttavia questa non è la soluzione corretta. Trovi questo valore solo perché optim termina in anticipo quando ha trovato una soluzione sufficientemente buona e i miglioramenti per una determinata dimensione del vettore $ \ beta, \ gamma $ stanno diventando piccoli.
Quando utilizzi l'ottimizzazione nidificata, troverai una soluzione più precisa con un $ R_0 $ molto vicino a 1.
Vediamo questo valore $ R_0 \ approx 1 $ perché è così che il modello (sbagliato) è in grado di ottenere questa variazione del tasso di crescita nella curva.
###
####
####
libreria (deSolve)
libreria (RColorBrewer)
#https: //en.wikipedia.org/wiki/Timeline_of_the_2019%E2%80%9320_Wuhan_coronavirus_outbreak#Cases_Chronology_in_Mainland_China
< infetto- c (45,62,121,198,291,440,571,830,1287,1975,
2744,4515,5974,7711,9692,11791,14380,17205,20440)
#Infected <- c (45,62,121,198,291,440,571,830,1287,1975,
# 2744,4515,5974,7711,9692,11791,14380,17205,20440,
# 24324,28018,31161,34546,37198,40171,42638,44653)
giorno <- 0: (length (Infected) -1)
N <- 1400000000 #pop della Cina
init <- c (S = N-Infected [1], I = Infected [1], R = 0)
# funzione modello
SIR2 <- funzione (ora, stato, parametri) {
par <- as.list (c (stato, parametri))
con (par, {
beta <- const / (1-1 / R0)
gamma <- const / (R0-1)
dS <- - (beta * (S / N)) * I
dI <- (beta * (S / N) -gamma) * I
dR <- (gamma) * I
elenco (c (dS, dI, dR))
})
}
### Due funzioni RSS per eseguire l'ottimizzazione in modo annidato
RSS.SIRMC2 Funzione < (R0, const) {
parametri <- c (const = const, R0 = R0)
out <- ode (y = init, times = day, func = SIR2, parms = parameters)
adatta <- out [, 3]
RSS <- sum ((Infected_MC - fit) ^ 2)
ritorno (RSS)
}
RSS.SIRMC <- funzione (const) {
ottimizzare (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = const) $ obiettivo
}
# wrapper per ottimizzare e restituire i valori stimati
getOptim <- function () {
opt1 <- ottimizza (RSS.SIRMC, inferiore = 0, superiore = 1)
opt2 <- ottimizza (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = opt1 $ minimo)
return (elenco (RSS = opt2 $ obiettivo, const = opt1 $ minimo, R0 = opt2 $ minimo))
}
# facendo il modello annidato per ottenere RSS
Infected_MC <- Infected
modnested <- getOptim ()
rss <- sapply (seq (0.3,0.5,0.01),
FUN = funzione (x) ottimizza (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = x) $ obiettivo)
trama (seq (0.3,0.5,0.01), rss)
ottimizzare (RSS.SIRMC2, inferiore = 1, superiore = 10 ^ 5, const = 0,35)
# Visualizza
modnested
### tracciare valori diversi R0
const <- modnested $ const
R0 <- modnested $ R0
# grafico
grafico (-100, -100, xlim = c (0,80), ylim = c (1,6 * 10 ^ 4), log = "",
ylab = "infetto", xlab = "giorni")
title (bquote (paste ("scenario's for different", R [0])), cex.main = 1)
### questo è ciò che la tua beta e gamma dal blog
beta = 0,6746089
gamma = 0,3253912
fit <- data.frame (ode (y = init, times = t, func = SIR, parms = c (beta, gamma))) $ I
linee (t, fit, col = 3)
# modello di trama con differenti R0
t <- seq (0,50,0.1)
for (R0 in c (modnested $ R0,1.07,1.08,1.09,1.1,1.11)) {
fit <- data.frame (ode (y = init, times = t, func = SIR2, parms = c (const, R0))) $ I
linee (t, fit, col = 1 + (modnested $ R0 == R0))
testo (t [501], adattato [501],
bquote (incolla (R [0], "=",. (R0))),
cex = 0.7, pos = 4, col = 1 + (modnested $ R0 == R0))
}
# osservazioni sulla trama
punti (giorno, infetto, cex = 0,7)
Se usiamo la relazione tra persone recuperate e infette $ R ^ \ prime = c (R_0-1) ^ {- 1} I $ allora vediamo anche l'opposto, vale a dire un grande $ R_0 $ di circa 18:
I <- c (45,62,121,198,291,440,571,830,1287,1975,2744,4515,5974,7711,9692,11791,14380,17205,20440, 24324,28018,31161,34546,37198,40171,42638 , 44653)
D <- c (2,2,2,3,6,9,17,25,41,56,80,106,132,170,213,259,304,361,425,490,563,637,722,811,908,1016,1113)
R <- c (12,15,19,25,25,25,25,34,38,49,51,60,103,124,171,243,328,475,632,892,1153,1540,2050,2649,3281,3996,4749)
Un <- I-D-R
grafico (A [-27], diff (R + D))
mod <- lm (diff (R + D) ~ A [-27])
dare:
> const
[1] 0,3577354
> const / mod $ coefficienti [2] +1
A [-27]
17.87653
Questa è una restrizione del modello SIR che modella $ R_0 = \ frac {\ beta} {\ gamma} $ dove $ \ frac {1} {\ gamma} $ è il periodo di tempo in cui qualcuno è malato (tempo da infetto a guarito) ma potrebbe non essere necessario che qualcuno sia contagioso. Inoltre, i modelli di compartimento sono limitati poiché l'età dei pazienti (quanto tempo si è ammalati) non viene presa in considerazione e ogni età dovrebbe essere considerata come un compartimento separato.
Ma in ogni caso. Se i numeri di wikipedia sono significativi (potrebbero essere messi in dubbio), solo il 2% degli attivi / infetti si riprende quotidianamente, e quindi il parametro $ \ gamma $ sembra essere piccolo (non importa quale modello usi).