Se $ X_i $ sono iid Normali (0,1), un campione da esso non avrà media campionaria 0 o deviazione standard campionaria 1 solo a causa della variazione casuale.

Ora considera cosa succede quando facciamo $ Z = \ frac {X- \ overline {X}} {s_X} $

Mentre lo facciamo ora avere media campione 0 e deviazione standard campione 1, ciò che non abbiamo è che $ Z $ viene distribuito normalmente.

In campioni di dimensioni da piccole a moderate, ha code corte, e curtosi sostanzialmente più piccola di un normale standard, infatti dalla simulazione per campioni di dimensione n = 10 sembra abbastanza simile a una beta scalata (4,4) (che è stata scalata per trovarsi in (-3,3)):

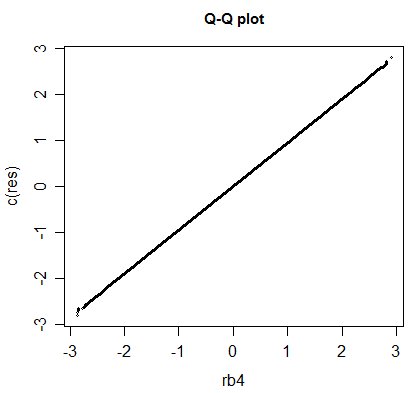
(L'asse x è un campione casuale di B (4,4) scalato a (-3,3). Ovviamente questo non significa che la forma di distribuzione è una beta (4,4).)

I valori in res sono stati generati come segue:

  res = replicate (100000, scale (rnorm (10)))  

Per i campioni di dimensione 5, il risultato sembra piuttosto una beta scalata (3 / 2,3 / 2).

Inoltre, i valori in ogni campione non sono più indipendenti, poiché sommano a 0 e i loro quadrati a $ n-1 $

Abbiamo quello

$$ X_i ^ * = \ frac {X_i} {s} - \ frac {\ bar X} {s} $$

La varianza del campione da un campione normale segue una distribuzione esatta,

$$ (n-1) s ^ 2 / \ sigma ^ 2 \ sim \ chi ^ 2_ {n-1} \ implica s ^ 2 \ sim \ frac {1} {n-1} \ chi ^ 2_ {n-1} \ implica s \ sim \ frac {1} {\ sqrt {n-1}} \ chi_ {n-1} $$

es $ s $ segue la radice quadrata di un chi quadrato diviso per i suoi gradi di libertà.

Ma anche se questo significa che $ \ frac {X_i} {s} $ è il rapporto tra una normale standard su la radice quadrata di un chi quadrato diviso per i suoi gradi di libertà, il numeratore non è indipendente dal denominatore, e quindi non possiamo dire che il rapporto segue la distribuzione $ t $ di uno Student (e personalmente Non conosco la sua distribuzione).

Per quanto riguarda il secondo termine, è noto che la media campionaria e la varianza campionaria sono variabili casuali indipendenti se e solo se il campione è costituito da normali indipendenti, che è la caso qui.

Inoltre, la media campionaria segue una distribuzione normale a media zero con varianza qui $ 1 / n $, quindi $ \ sqrt {n} \ bar X $ segue una normale standard.

Quindi abbiamo quel $$ \ frac {\ sqrt {n} \ bar X} {s} \ sim t \ implica \ frac {\ bar X} {s} \ sim \ frac {1} {\ sqrt {n}} t $$

es il secondo termine di $ X_i ^ * $ segue una distribuzione $ t $ di uno studente in scala

Quindi in tutto

$$ X ^ * _ i = \ frac {Z_i} {\ sqrt {\ chi ^ 2_ {n-1} / (n-1)}} - \ frac {1} {\ sqrt {n}} t $$

dove ho hanno usato il simbolo $ Z $ per denotare una variabile casuale che segue una normale standard. Il primo termine non è $ t $ di uno studente e inoltre non è indipendente dal secondo termine. Messo insieme non sembra molto normale o nemmeno della distribuzione di uno studente.

Le variabili normali standard originali hanno VERO media 0 (E (X) = 0) e sono indipendenti. Prendendone un insieme e dividendoli per la loro deviazione standard, li standardizzi, ma il risultato, ironia della sorte, non è normale. Sono dipendenti (perché condividono il denominatore) e in realtà hanno distribuzioni t. Quindi, se vuoi lo standard normale, resta con rnorm (5).

Ho appena eseguito alcuni esperimenti. Sembra che dopo la scala di nuovo, sei più vicino a ottenere alcuni dati con $ \ mu = 0 $ e $ \ sigma = 1 $.

  set.seed (123) x <- rnorm (1000,0,1) mean (x) sd (x) y<-scale (x) mean (y) sd (y)  

Risultati:

  > mean (x) [1] 0,01612787 > sd (x) [1] 0,991695> y<-scale (x) > mean ( y) [1] -8.235085e-18> sd (y) [1] 1  

Dimostrazione intuitiva per controesempio

Ci sono già alcune risposte generali che coprono la domanda, ma personalmente trovo il seguente ragionamento più facile da seguire.

Supponi che la dimensione del tuo campione sia 1 .

La tua definizione di $ X ^ * $ è la seguente

$$ X ^ * = \ frac {x- \ bar x} {sd (x)} $$

Poiché la dimensione del campione è 1, abbiamo $ \ bar x = x $ , quindi per qualsiasi $ x $ l'espressione si riduce a

$$ X ^ * = \ frac {\ bar x- \ bar x} {sd (x)} = \ frac {0} {0} $$

Poiché $ X ^ * $ non è chiaramente distribuito normalmente per la dimensione del campione 1, non può sicuramente avere una distribuzione normale standard in generale.