Una delle soluzioni più semplici riconosce che i cambiamenti tra probabilità piccole (come 0,1) o i cui complementi sono piccoli (come 0,9) sono solitamente più significativi e meritano più peso rispetto ai cambiamenti tra probabilità medie ( come 0,5).

Ad esempio, una modifica da 0,1 a 0,2 (a) raddoppia la probabilità mentre (b) modifica la probabilità complementare solo di 1/9 (facendola cadere da 1-0,1 = 0,9 a 1 Da -0,2 a 0,8), mentre una variazione da 0,5 a 0,6 (a) aumenta la probabilità solo del 20% mentre (b) diminuisce la probabilità complementare solo del 20%. In molte applicazioni la prima modifica è, o almeno dovrebbe essere, considerata grande quasi il doppio della seconda.

In qualsiasi situazione in cui sarebbe altrettanto significativo usare una probabilità (che qualcosa si verifichi ) o il suo complemento (cioè la probabilità che qualcosa non si verifichi), dobbiamo rispettare questa simmetria.

Queste due idee - di rispettare la simmetria tra le probabilità $ p $ e i loro complementi $ 1- p $ e di esprimere i cambiamenti in modo relativo piuttosto che assoluto - suggerire che quando si confrontano due probabilità $ p $ e $ p '$ dovremmo tenere traccia sia dei loro rapporti $ p' / p $ sia dei rapporti dei loro complementi $ ( 1-p) / (1-p ') $. Quando si tengono traccia dei rapporti è più semplice utilizzare i logaritmi, che convertono i rapporti in differenze. Ergo, un buon modo per esprimere una probabilità $ p $ a questo scopo è usare $$ z = \ log p - \ log (1-p), $$ che è noto come quota di registro o logit di $ p $. Le quote log adattate $ z $ possono sempre essere riconvertite in probabilità invertendo il logit; $$ p = \ exp (z) / (1+ \ exp (z)). $$ L'ultima riga del codice sotto mostra come si fa.

Questo ragionamento è piuttosto generale: porta a una buona procedura iniziale predefinita per esplorare qualsiasi insieme di dati che coinvolge le probabilità. (Sono disponibili metodi migliori, come la regressione di Poisson, quando le probabilità sono basate sull'osservazione di rapporti di "successi" rispetto al numero di "prove", perché le probabilità basate su più prove sono state misurate in modo più affidabile. Non sembra essere il caso qui, in cui le probabilità sono basate su informazioni ottenute. Si potrebbe approssimare l'approccio di regressione di Poisson utilizzando i minimi quadrati ponderati nell'esempio seguente per consentire dati più o meno affidabili.)

Diamo un'occhiata a un esempio.

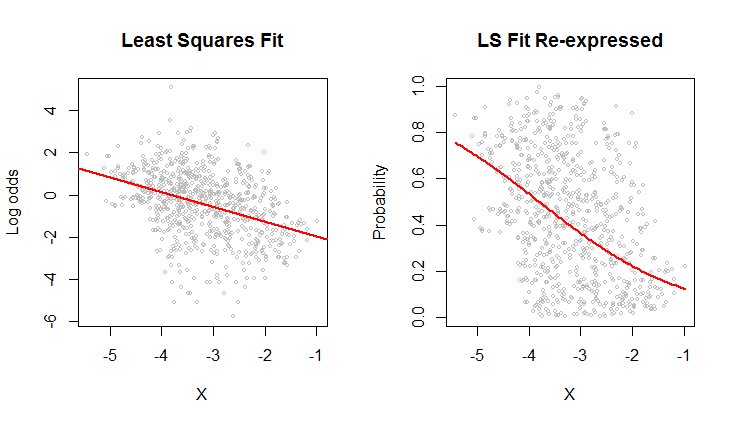
Il grafico a dispersione a sinistra mostra un dataset (simile a quello nella domanda) tracciato in termini di probabilità di log. La linea rossa è la misura dei minimi quadrati ordinari. Ha un $ R ^ 2 $ basso, che indica molta dispersione e una forte "regressione alla media": la retta di regressione ha una pendenza minore dell'asse maggiore di questa nuvola di punti ellittica. Questo è un ambiente familiare; è facile da interpretare e analizzare utilizzando la funzione lm di R o equivalente.

Lo scatterplot a destra esprime i dati in termini di probabilità , come sono stati originariamente registrati. Viene tracciato lo stesso adattamento: ora sembra curvo a causa del modo non lineare in cui le probabilità logaritmiche vengono convertite in probabilità.

Nel senso di errore quadratico medio radice em> in termini di quote logaritmiche, questa curva è la migliore adatta.

Per inciso, la forma approssimativamente ellittica della nuvola a sinistra e il modo in cui traccia la linea dei minimi quadrati suggeriscono che il modello di regressione dei minimi quadrati è ragionevole: i dati possono essere adeguatamente descritti da una relazione lineare-- fornito vengono utilizzate le quote logaritmiche e la variazione verticale attorno alla linea è all'incirca della stessa dimensione indipendentemente dalla posizione orizzontale (omoschedasticità). (Ci sono alcuni valori insolitamente bassi nel mezzo che potrebbero meritare un esame più attento.) Valutalo in modo più dettagliato seguendo il codice seguente con il comando plot (fit) per vedere alcune diagnostiche standard. Questo da solo è un motivo valido per utilizzare le probabilità di log per analizzare questi dati invece delle probabilità.

  ## Leggi i dati da una tabella di (X, Y) = (X, probabilità) coppie. # x <- read.table ("F: /temp/data.csv", sep = ",", col.names = c ("X", " Y ")) ## Definisce le funzioni per convertire tra probabilità` p` e log odds `z`. # (Quando alcune probabilità effettivamente sono uguali a 0 o 1, un piccolo aggiustamento - dato da un valore # positivo di" e` - deve essere applicato per evitare quote logaritmiche infinite.) # logit <- funzione (p, e = 0) {x <- (p-1/2) * (1-e) + 1/2; log (x) - log (1-x)} logistica <- funzione (z, e = 0) {y <- exp (z) / (1 + exp (z)); (y-1/2) / (1-e) + 1/2} ## Misura le probabilità logaritmiche usando i minimi quadrati. # b <- coef (misura <- lm (logit (x $ Y) ~ x $ X) ) ## Traccia i risultati in due modi. # Par (mfrow = c (1,2)) plot (x $ X, logit (x $ Y), cex = 0.5, col = "Gray", main = "Least Squares Fit ", xlab =" X ", ylab =" Log odds ") abline (b, col =" Red ", lwd = 2) plot (x $ X, x $ Y, cex = 0.5, col =" Gray ", main = "LS Fit Re-espresso", xlab = "X", ylab = "Probability") curva (logistica (b [1] + b [2] * x), col = "Red", lwd = 2, aggiungi = TRUE)  

Data l'inclinazione dei dati con x, la prima cosa ovvia da fare è utilizzare una regressione logistica ( wiki link). Quindi sono con Whuber su questo. Dirò che $ x $ da solo mostrerà un forte significato ma non spiegherà la maggior parte della devianza (l'equivalente della somma totale dei quadrati in un OLS). Quindi si potrebbe suggerire che esiste un'altra covariata oltre a $ x $ che aiuta il potere esplicativo (ad esempio le persone che fanno la classificazione o il metodo utilizzato), I tuoi dati $ y $ sono già [0,1] però: sai se loro rappresentano probabilità o rapporti di occorrenza? Se è così, dovresti provare una regressione logistica usando il tuo $ y $ non trasformato (prima che siano rapporti / probabilità).

L'osservazione di Peter Flom ha senso solo se la tua y non è una probabilità. Controlla plot (density (y)); rug (y) in diversi bucket di $ x $ e vedi se vedi una distribuzione Beta che cambia o semplicemente esegui betareg . Nota che la distribuzione beta è anche una distribuzione familiare esponenziale e quindi dovrebbe essere possibile modellarla con glm in R.

Per darti un'idea di cosa intendevo per logistica regressione:

  # la relazione 'reale' dove y viene interpretata come probabilità di successo = runif (400) x = -2 * (log (y / (1-y)) - 2 ) + rnorm (400, sd = 2) glm.logit = glm (y ~ x, famiglia = binomiale); diagramma di riepilogo (glm.logit) (y ~ x); richiedono (lontano); grid () points (x, ilogit (coef (glm.logit)% *% rbind (1.0, x)), col = "red") tt = runif (400) # un esempio della tua regressione non trasformatanewy = ifelse (tt < y, 1, 0) glm.logit = glm (newy ~ x, family = binomial); riepilogo (glm.logit) # se non c'è una buona corrispondenza nelle probabilità della coda prova una funzione di collegamento diversa o un sovracampionamento con correzione (sarà peggio qui, ma forse non nei tuoi dati) glm.probit = glm (y ~ x, famiglia = binomiale (link = probit)); riepilogo (glm.probit) glm.cloglog = glm (y ~ x, family = binomial (link = cloglog)); riepilogo (glm.cloglog)  

MODIFICA: dopo aver letto i commenti:

Dato che "I valori y sono probabilità di appartenere a una certa classe, ottenute dalla media delle classificazioni eseguite manualmente dalle persone", consiglio vivamente di fare una regressione logistica sui dati di base. Ecco un esempio:

Supponiamo che tu stia osservando la probabilità che qualcuno accetti una proposta ($ y = 1 $ d'accordo, $ y = 0 $ in disaccordo) dato un incentivo $ x $ compreso tra 0 e 10 (potrebbe essere trasformato in log, ad esempio retribuzione). Ci sono due persone che propongono l'offerta ai candidati ("Jill e Jack"). Il modello reale è che i candidati hanno un tasso di accettazione di base e che aumenta all'aumentare dell'incentivo. Ma dipende anche da chi propone l'offerta (in questo caso diciamo che Jill ha maggiori possibilità di Jack). Supponiamo che insieme chiedano 1000 candidati e raccolgano i loro dati di accettazione (1) o rifiuto (0).

  require (faraway) people = c ("Jill", "Jack") proposer = sample (people, 1000, replace = T) incentive = runif (1000, min = 0, max = 10) noise = rnorm (1000, sd = 2) # la probabilità base di concordare è di circa il 12% (ilogit (-2)) concorda = ilogit (-2 + 1 * incentivo + ifelse (proposer == "Jill", 0, -0,75) + rumore) tt = runif (1000) viewedAgrees = ifelse (tt < concorda, 1,0) glm.logit = glm (viewedAgrees ~ incentivo + proposer, family = binomial); riepilogo (glm.logit) 

Dal riepilogo puoi vedere che il modello si adatta abbastanza bene. La devianza è $ \ chi ^ 2_ {n-3} $ (lo standard di $ \ chi ^ 2 $ è $ \ sqrt {2.df} $). Che si adatta e batte un modello con una probabilità fissa (la differenza nelle deviazioni è di diverse centinaia con $ \ chi ^ 2_ {2} $). È un po 'più difficile da disegnare dato che ci sono due covariate qui, ma hai un'idea.

  xs = coef (glm.logit)% *% rbind (1, incentive, as.factor (proposer)) ys = as.vector (unlist (ilogit (xs))) plot (ys ~ incentive, type = "n"); richiedono (lontano); grid () points (incentive [proposer == "Jill"], ys [proposer == "Jill"], col = "red") points (incentive [proposer == "Jack"], ys [proposer == "Jack "], col =" blue ")  

Come puoi vedere, Jill ha difficoltà a ottenere un buon tasso di successo rispetto a Jack, ma questo scompare con l'aumento dell'incentivo.

In pratica dovresti applicare questo tipo di modello ai tuoi dati originali. Se il tuo output è binario, mantieni 1/0, se è multinomiale hai bisogno di una regressione logistica multinomiale. Se ritieni che la fonte aggiuntiva di varianza non sia il raccoglitore di dati, aggiungi un altro fattore (o variabile continua) qualunque cosa pensi abbia senso per i tuoi dati. I dati vengono prima, seconda e terza, solo allora entra in gioco il modello.

Il modello di regressione lineare non è adatto per i dati. Ci si potrebbe aspettare di ottenere qualcosa del genere dalla regressione:

ma rendendosi conto di cosa fa OLS, è ovvio che questo non è ciò che si otterrà. Un'interpretazione grafica dei minimi quadrati ordinari è che riduce al minimo la distanza verticale al quadrato tra la linea (iperpiano) e i dati. Ovviamente la linea viola che ho sovrapposto ha degli enormi residui da $ x \ in (-7,4.5) $ e di nuovo sull'altro lato di 3. Questo è il motivo per cui la linea blu si adatta meglio della viola.

Poiché Y è limitato da 0 e 1, la normale regressione dei minimi quadrati non è adatta. Potresti provare la regressione beta. In R c'è il pacchetto betareg .

Prova qualcosa di simile

  install.packages ("betareg") libreria (betareg) betamod1 <- betareg (y ~ x, data = DATASETNAME)  

maggiori informazioni

MODIFICA: se desideri un resoconto completo della regressione beta, dei suoi vantaggi e svantaggi, consulta Uno spremiagrumi migliore : Regressione di massima verosimiglianza con variabili dipendenti distribuite beta di Smithson e Verkuilen

Per prima cosa potresti voler sapere esattamente cosa fa un modello lineare. Cerca di modellare una relazione della forma

$$ Y_i = a + bX_i + \ epsilon_i $$

Dove $ \ epsilon_i $ soddisfa determinate condizioni (eteroschedasticità, varianza uniforme e indipendenza - wikipedia è un buon inizio se questo non suona un campanello). Ma anche se queste condizioni vengono verificate, non c'è assolutamente alcuna garanzia che questa sia la "soluzione migliore" nel senso che stai cercando: OLS sta solo cercando di ridurre al minimo l'errore nella direzione Y, che è ciò che sta facendo nel tuo caso, ma non è quella che sembra la soluzione migliore.

Se un modello lineare è davvero quello che stai cercando, potresti provare a trasformare un po 'le tue variabili in modo che OLS possa effettivamente essere adattato, o semplicemente provare un altro modello del tutto. Potresti voler esaminare PCA o CCA, o se sei davvero deciso a utilizzare un modello lineare, prova la soluzione minimi quadrati totali, che potrebbe fornire un "adattamento" migliore, in quanto consente errori in entrambe le direzioni.