TQuesto diagramma di Venn mostra una situazione in cui la possibilità di intersezione reciproca è zero:

Da $ \ Pr (E \ cap F) = 1/3 $ deduciamo che tutta questa probabilità risiede nella sovrapposizione dei $ E $ e $ F $ , ma non nella reciproca sovrapposizione di tutti e tre i dischi. ci permette di aggiornare il diagramma:

Applicando lo stesso ragionamento a $ \ Pr (F \ cap G) = \ Pr (E \ cap G) = 1/3, $ otteniamo un Venn diagramma che mostra tutte le informazioni nella domanda:

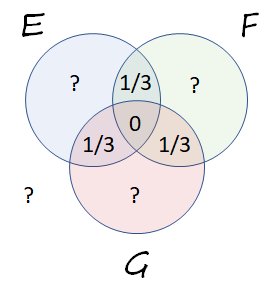
L ' assioma della probabilità totale afferma la somma di tutte le probabilità (inclusa la probabilità per il complemento di $ E \ cup F \ cup G, $ mostrato in basso a sinistra) è $ 1. $

Un assioma di probabilità ancora più elementare afferma che tutte le probabilità devono essere non negative. Ma poiché $ 1/3 + 1/3 + 1/3 + 0 = 1, $ tutte le probabilità possibili sono già visualizzate. Le probabilità rimanenti deve essere zero, il che significa l'immagine può essere completata solo in questo modo:

Infine, un terzo assioma (lo stesso usato nella seconda fase di compilazione del diagramma di Venn) afferma che la probabilità che $ E $ sia uguale alla somma dei probabilità delle sue quattro parti, perché sono disgiunte. Quindi, iniziando con la probabilità centrale e muovendosi in senso antiorario attorno al disco che raffigura $ E, $ span >

$$ \ Pr (E) = 0 + 1/3 + 0 + 1/3 = 2/3. $$

Una morale che vale la pena ricordare:

Disegna i diagrammi di Venn in piena generalità in modo che mostrino tutte le possibili intersezioni degli insiemi, anche quando sai che alcune delle probabilità sono zero.

Questo ti aiuta a tenere traccia di tutte le informazioni in modo sistematico.(È anche concettualmente più accurato, perché gli insiemi di probabilità zero non devono essere non vuoti!)

Se provi a riempire il diagramma di Venn, non puoi inserire voci diverse da zero all'interno di regioni diverse da quelle rappresentate da intersezioni a coppie.Formeranno da soli lo spazio campione, il che significa $$ \ mathbb P (E) = \ mathbb P (E \ cap F) + \ mathbb P (E \ cap G) = 2/3 $$

La risposta alla domanda "Sai determinare $ P (E) $ ?" è Yes.

Dati eventi $ E, F, G $ definiti su uno spazio campione $ \ Omega $ , lo sappiamo \ begin {align} &E \ cap F \ cap G \\ &E \ cap F \ cap G ^ c \\ &E \ cap F ^ c \ cap G \\ &E \ cap F ^ c \ cap G ^ c \\ &E ^ c \ cap F \ cap G \\ &E ^ c \ cap F \ cap G ^ c \\ &E ^ c \ cap F ^ c \ cap G \\ &E ^ c \ cap F ^ c \ cap G ^ c \\ \ end {align} sono eventi $ 8 $ che si escludono a vicenda la cui unione è $ \ Omega $ . Pertanto, la somma delle probabilità di questi $ 8 $ eventi è $ 1 $ . Ora, ci viene detto che $ E, F, G $ non può verificarsi contemporaneamente, cioè $ E \ cap F \ cap G = \ emptyset $ e così via $ P (E \ cap F \ cap G) = 0 $ . Anche questo ci viene detto \ begin {align} P (E \ cap F) & = P (E \ cap F \ cap G) + P (E \ cap F \ cap G ^ c) = \ frac 13 \\ P (E \ cap G) & = P (E \ cap F \ cap G) + P (E \ cap F ^ c \ cap G) = \ frac 13 \\ P (F \ cap G) & = P (E \ cap F \ cap G) + P (E ^ c \ cap F \ cap G) = \ frac 13 \ end {align} dove possiamo sentirci a nostro agio sulla somma nel mezzo in ogni equazione meditando sul fatto che la probabilità dell ' unione di due eventi che si escludono a vicenda è la somma delle probabilità dei due eventi. Poiché $ P (E \ cap F \ cap G) = 0 $ , concludiamo che \ begin {align} P (E \ cap F) & = P (E \ cap F \ cap G ^ c) = \ frac 13 \\ P (E \ cap G) & = P (E \ cap F ^ c \ cap G) = \ frac 13 \\ P (F \ cap G) & = P (E ^ c \ cap F \ cap G) = \ frac 13 \ end {align}

Tuttavia, degli $ 8 $ eventi che si escludono a vicenda elencati sopra la cui unione è $ \ Omega $ ,abbiamo identificato tre eventi le cui probabilità si sommano a $ 1 $ e quindi gli altri $ 5 $ eventi (uno diche è $ E \ cap F \ cap G $ ) deve avere probabilità $ 0 $ .Di conseguenza, \ begin {align} P (E) & = P (E \ cap F \ cap G) + P (E \ cap F \ cap G ^ c) + P (E \ capF ^ c \ cap G) + P (E \ cap F ^ c \ cap G ^ c) \\ & = 0 + \ frac 13 + \ frac 13 + 0 \\ & = \ frac 23 \ end {align} Per simmetria (o per una ripetizione di forza bruta degli argomenti precedenti mutatis mutandis ), possiamo concludere che $ E, F, G $ tutti hanno probabilità $ \ frac 23 $ .

Possiamo pensarlo in questo modo?

P (MI SOL) = P (MI SOL) = P (MI ∩ SOL) = 1/3

P (MI SOL) + P (MI SOL) + P (MI ∩ SOL) = 1

Significa che la probabilità che l'evento E si verifichi da solo è zero, il che significa che può accadere solo con F o G e non può accadere con entrambi.

P (MI) = P (MI ∩ FA) + P (MI ∩ SOL) = 1/3 + 1/3 = 2/3

Poiché gli eventi $ (E, F) $ , $ (E, G) $ $ (F, G) $ si escludono a vicenda e sommando a uno possiamo usare la legge del problema totale: $$ P (E) = P (E, F) + P (E, G) = \ tfrac {2} {3} $$ Poiché $ P (E \ mid E, F) P (E, F) = P (E, F) $ , idem per $ E, G $ e $ P (E \ mid F, G) = 0 $ .