Spiacenti, sono un po 'nuovo qui, quindi scusami se questo non aiuta troppo.

La US Social Security Administration conserva i registri di nascite e morti e ha le loro informazioni disponibili per l'acquisto un prezzo alto): Qui

Tuttavia ho trovato una fonte che afferma di averlo acquistato e lo offre gratuitamente (oltre a offrire i dati ordinati per data sul sito ): Qui

Suppongo che tu possa semplicemente usarlo come campione e passare attraverso tutti i dati con uno script e scoprire quante persone muoiono effettivamente il giorno del loro compleanno. Lo farei da solo ma mi rimangono 20 minuti per il download (sono circa 1,5 GB), quindi cercherò di ricontattarti sulle statistiche io stesso se trovo il tempo di scrivere uno script.

Ovviamente gli Stati Uniti non possono rappresentare l'intera popolazione mondiale, ma è un buon inizio. Presumo che vedrai un tasso più elevato di decessi nei compleanni a causa dei "problemi del primo mondo" perché stiamo usando gli Stati Uniti e penso che l'effetto sarebbe meno visibile in tutto il mondo ...

Aggiornamento - Numeri: D

Ho esaminato il file principale della morte della previdenza sociale dalla fonte gratuita, quindi non c'è modo di sapere se le informazioni sono valide. Tuttavia, data la dimensione che sono ~ 3 Gigabyte ciascuno e che non c'è motivo per nessuno di falsificare questo tipo di file ... presumo che siano validi.

Puoi vedere il codice che Lo leggevo qui: http://pastebin.com/9wUFuvpN

È scritto in C #, legge le righe dell'indice di morte una per una e poi analizza la data utilizzando regex. Ho pensato che il file fosse fondamentalmente questo formato:

  `(Social Security Number) (First Name) (LastName) (Middle Name) (Some Letter) (MM-DD-YYYY of Death) (MM-GG-AAAA di nascita) " 

Ho fatto in modo che le espressioni regolari selezionassero l'ultima parte per le date di nascita / morte, controlla se uno qualsiasi dei campi è solo 0 (che presumo significhi che la previdenza sociale non ha potuto ottenere un mese / data valido per il record) e scartare gli 0. Quindi controllerà se il giorno di nascita e il mese di nascita corrispondono al giorno della morte / mese di morte e lo aggiungerà al conteggio dei morti per compleanno. Aggiungerà tutti i record che non sono 0 al conteggio delle morti.

Fornisce i risultati in questo formato:

Morti al compleanno / Linee di morte totali esaminate - Persone con uno 0 in uno qualsiasi dei loro record

Sarebbe fantastico se qualcuno potesse ricontrollare quel codice, poiché ho trovato parecchi errori che ho fatto prima e potevo solo dire perché i miei risultati non avevano senso statistico.

Ecco l'output della console: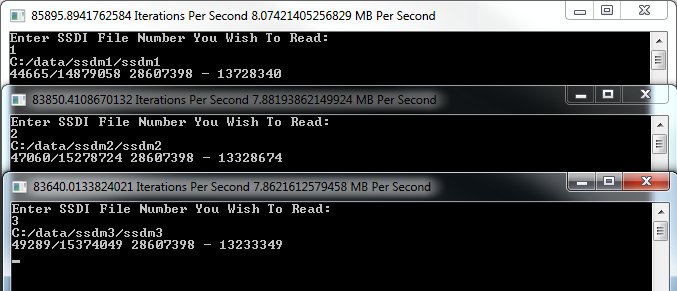

Facendo un po 'di matematica ...

• Il file 1 aveva 44665 Morti in un compleanno su 14879058 Morti in totale
• File 2 ha avuto 47060 Morti in un compleanno su 15278724 Morti in totale
• File 3 ha avuto 49289 Morti in un compleanno su 15374049 Morti in totale
• In totale abbiamo 141014 morti in un compleanno su 45531831.

Quindi abbiamo una probabilità dello 0,3097% di morire il giorno di un compleanno mentre statisticamente (1 / 365) ci indurrebbe a credere che ci sia solo ~ 0,27397% di possibilità di morire per un compleanno. Questo è effettivamente un aumento del 13% della possibilità di morte per un compleanno da 1/365. Ovviamente questo campione è solo per gli americani e ha solo 45 milioni di record, sono sicuro che le organizzazioni che originariamente hanno pubblicato il loro articolo hanno avuto accesso a indici di morte molto più affidabili e più ampi. Tuttavia, penso che sia davvero valido che la morte in un compleanno sia più probabile della morte in qualsiasi altro giorno.

Ecco un articolo del Time che cita salti nei motivi della morte nei compleanni: Articolo

Modifica 2: @cbeleites ha sottolineato che ho dimenticato di tenere conto delle morti nello stesso giorno, il che sarebbe un fattore enorme nell'aumento dei decessi nei compleanni. A rigor di termini i miei dati sono ancora validi ma non ho buttato via se una persona è morta lo stesso giorno in cui è nata. È interessante notare che i miei risultati non sono stati influenzati troppo pesantemente da questo errore, quindi sembra che questi record non includano la morte il primo giorno. Lo esaminerò più tardi. Penso che ci sarebbero statistiche molto interessanti che posso cercare come la morte nei giorni del mese e fare una mappa termica di qualche tipo. Probabilmente proverò a farlo prima o poi ...

Possiamo essere ancora più precisi dei dati di @Mike Shi: il più pericoloso di tutti i compleanni è il primo in assoluto.

I tassi di mortalità del primo giorno segnalati sono intorno 0,2% per i paesi industrializzati e 0,8% in media per tutti i paesi. Ciò significa che il rischio di morire il giorno della nascita è almeno pari al rischio di morire in uno qualsiasi dei giorni di nascita successivi *.

* Penso che sia un presupposto sicuro che i decessi del primo giorno non compaiano nel file di @Mark Shi, poiché i tassi di mortalità del primo giorno negli Stati Uniti sarebbero dello 0,3% ( altra fonte: 0,26%). Che è quasi il tasso di mortalità totale al giorno della nascita nel file di sicurezza sociale. Quindi o i bambini che muoiono il giorno della nascita non ottengono un numero di previdenza sociale o morire in un giorno di nascita> 1 anno è estremamente improbabile.

nota a margine:
Ci sono altri giorni, come il Natale e il Capodanno, che sono noti per avere anche tassi di mortalità superiori alla media.

Ecco un motivo per cui la probabilità di morte nel giorno del compleanno potrebbe essere più alta rispetto agli altri giorni: i compleanni sono giorni carichi di emozioni. Inoltre, le persone tendono a festeggiarlo in qualche modo .. Quindi c'è un eccesso di fattori (rispetto al solito stile di vita della persona) che aumentano lo stress biologico (emozioni in eccesso, eccesso di alcol, eccesso di cibo, eccesso di ballo, eccesso di banjee jumping ecc.). Statisticamente parlando, questa situazione aumenta le possibilità di morire il giorno di un compleanno, poiché intensifica i problemi di salute che una persona può avere o perché espone la persona a situazioni e rischi per i quali la persona è inesperta.

La probabilità che un neonato muoia entro un anno può essere trovata nelle tabelle della vita. Ad esempio, puoi controllare le tabelle della vita periodica e guardare la colonna $ q_x $ per $ x = 0 $ nel database della mortalità umana. Questo non è esattamente quello che vuoi, ma ti darà un'idea.

Oltre alle altre eccellenti risposte, c'è un punto in cui nessuno di loro ha discusso: i compleanni non sono distribuiti uniformemente nel corso dell'anno e nemmeno i giorni di morte. Ciò cospira in modo tale che la probabilità "statistica" sia not 1/365. Per avere un'idea di questo effetto, ipotizziamo innanzitutto che siano entrambi pressoché uniformi, solo il 29 febbraio ha una probabilità 1/4 degli altri. Questo dà $$ 365 p + \ frac14 p = 1 $$ quindi $ p = 0,002737851 $ . Ciò porta a probabilità di nascita e morte nello stesso giorno pari a $ 356 \ cdot p ^ 2 + (p / 4) ^ 2 = 0,002736445 > 0,00273224 = \ frac1 {366} $ span> che è il valore minimo possibile (con 366 giorni).

Con un po 'più di generalità, siano $ p_i, i = 1, \ dotsc, n $ le probabilità di compleanno e $ q_i, i = 1, \ dotsc, n $ le probabilità del giorno della morte, per un anno con $ n $ giorni. Quindi, se il compleanno e il giorno di morte di una persona sono statisticamente indipendenti, lo troveremo $$ \ DeclareMathOperator {\ P} {\ mathbb {P}} \ P (\ text {Nascita e morte nello stesso giorno}) = \ sum_ {i = 1} ^ n p_i q_i $$ quindi se $ p_i = q_i $ allora quello è $ \ sum_i p_i ^ 2 $ . Questa è una quantità nota (in biologia) come indice dei Simpson di (bio) diversità. Il suo inverso potrebbe quindi essere preso come "numero effettivo di giorni (in un anno)"! Il valore minimo di $ \ sum_i p_i ^ 2 $ è $ 1 / n $ . Per vederlo usa la convessità.

Ma supponendo che $ p_i = q_i $ sia piuttosto eccessivo, vediamo prima alcuni dati, le probabilità di compleanno per la Norvegia calcolate dai dati di ssb.no:

Chiaramente non uniforme, il valore anomalo più alto è 1. luglio. Non è reale, è causato da immigrati senza un compleanno documentato registrato in quella data. Un massimo in primavera, intorno all'inizio di aprile, un altro massimo in autunno, a settembre. L'indice Simpson calcolato da questo è $ 0,002750224 $ e l'inverso è $ 363.6067 $ , quindi il valore "effettivo numero di compleanni "è di circa 363 e mezzo, piuttosto vicino a 366. Quindi la disuniformità forse non è così importante. È più difficile trovare dati per il giorno della morte, ma ho trovato il giornale (in norvegese) (questa è la rivista ufficiale dell'associazione medica norvegese) riportano circa il 12% in più di tasso di morte in inverno rispetto in estate. Segnalano anche un lieve aumento del rischio di morte il lunedì! In effetti, i confronti internazionali riportati da quel documento mostrano che l'eccessiva mortalità invernale è più bassa in Scandinavia, in paesi come l'Irlanda o l'Inghilterra è circa il doppio. Potrebbe essere sorprendente, potrebbe avere a che fare con noi scandinavi che abbiamo case più calde e meglio isolate?

Da questo possiamo ricostruire una distribuzione del giorno della morte. Considero la metà dell'inverno novembre-aprile. Quindi possiamo calcolare $$ p_w = 1,12 p_s \\ (182 \ cdot 1.12 + 184) p_s = 1 $$ che porta a $ p_s = 0.002578383, p_w = 0.002887789 $ e infine $ \ sum_i p_i q_i = 0.00273151 $ , il suo inverso, il "numero effettivo di giorni" è 366,1, molto vicino a 366! L'anticorrelazione ( $ \ rho (p_i, q_i) = - 0.06 $ ) sembra compensare la non uniformità in modo tale che potremmo anche assumere l'uniformità (e la distribuzione uguale per il compleanno e il giorno della morte). Questo è abbastanza interessante.

MODIFICA: ecco un documento pubblicato sulla non uniformità nel problema del compleanno.

1 su 365 sarebbe la quota corretta, perché hai la garanzia di morire in un giorno su 365 giorni all'anno ... Pertanto, le probabilità sono 1 su 365.