È insolito non inserire un'intercetta e generalmente sconsigliabile: dovresti farlo solo se sai che è 0, ma penso che (e il fatto che non puoi confrontare $ R ^ 2 $ per accoppiamenti con e senza intercetta) è già ben e veramente coperto (se forse un po 'sopravvalutato nel caso dell'intercetta 0); Voglio concentrarmi sul tuo problema principale, che è che hai bisogno che la funzione adattata sia positiva, anche se torno al problema dell'intercetta 0 in parte della mia risposta.

Il modo migliore per ottenere sempre adattamento positivo è adattarsi a qualcosa che sarà sempre positivo; in parte ciò dipende dalle funzioni che devi adattare.

Se il tuo modello lineare era in gran parte conveniente (piuttosto che derivare da una relazione funzionale nota che potrebbe derivare da un modello fisico, diciamo), allora tu potrebbe invece funzionare con il tempo di log; il modello adattato è quindi garantito come positivo in $ t $. In alternativa, potresti lavorare con la velocità piuttosto che con il tempo, ma poi con gli adattamenti lineari potresti avere un problema con velocità piccole (tempi lunghi).

Se sai che la tua risposta è lineare nei predittori, puoi tentare di adattare una regressione vincolata, ma con la regressione multipla la forma esatta di cui hai bisogno dipenderà dalle tue x particolari (non esiste un vincolo lineare che funzionerà per tutti i $ x $), quindi è un bit ad-hoc.

Puoi anche guardare i GLM che possono essere usati per adattare i modelli che hanno valori adattati non negativi e possono (se necessario) anche avere $ E (Y) = X \ beta $ .

Ad esempio, si può adattare una gamma GLM con collegamento identità. Non dovresti finire con un valore adattato negativo per nessuna delle tue x (ma potresti forse avere problemi di convergenza in alcuni casi se forzi il collegamento di identità dove realmente non si adatta).

Ecco un esempio: il set di dati cars in R, che registra la velocità e le distanze di arresto (la risposta).

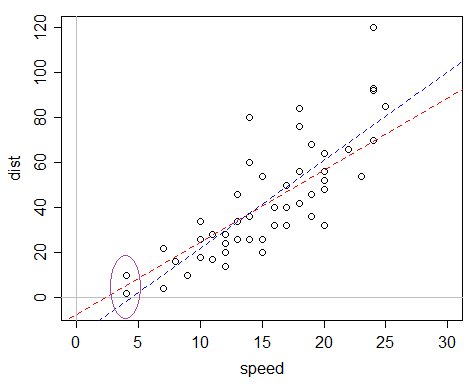
Si potrebbe dire "oh, ma la distanza per la velocità 0 è garantita essere 0, quindi dovremmo omettere l'intercetta" ma il problema con questo ragionamento è che il modello è specificato male in diversi modi e quell'argomento funziona solo bene abbastanza quando il modello non è specificato male - un modello lineare con 0 intercetta non si adatta affatto bene in questo caso, mentre uno con un'intercetta è in realtà un'approssimazione decente anche se in realtà non è "corretto".

Il problema è che, se si adatta una normale regressione lineare, l'intercetta adattata è piuttosto negativa, il che fa sì che i valori stimati siano negativi.

La linea blu è la vestibilità OLS; il valore adattato per i valori x più piccoli nel set di dati è negativo. La linea rossa è la gamma GLM con collegamento di identità: pur avendo un'intercetta negativa, ha solo valori adattati positivi. Questo modello ha una varianza proporzionale alla media, quindi se trovi che i tuoi dati sono più distribuiti con l'aumentare del tempo previsto, potrebbe essere particolarmente adatto.

Quindi questo è un possibile approccio alternativo che potrebbe valere la pena provare. È quasi facile come inserire una regressione in R.

Se non hai bisogno del collegamento di identità, potresti considerare altre funzioni di collegamento, come il collegamento di registro e il collegamento inverso, che si riferiscono alle trasformazioni già discusso, ma senza la necessità di una trasformazione effettiva.

Poiché le persone di solito lo chiedono, ecco il codice per il mio grafico:

  plot (dist ~ speed, data = cars, xlim = c (0, 30), ylim = c (-5,120)) abline (h = 0, v = 0, col = 8) abline (glm (dist ~ speed, data = cars, family = Gamma (link = identity)), col = 2 , lty = 2) abline (lm (dist ~ speed, data = cars), col = 4, lty = 2)  

(L'ellisse è stata aggiunta a mano in seguito, sebbene sia abbastanza facile da fare anche in R)

Risposta breve alla domanda nel titolo: (quasi) MAI. Nel modello di regressione lineare $$ y = \ alpha + \ beta x + \ epsilon $$ , se imposti $ \ alpha = 0 $ , allora dici di SAPERE che il valore atteso di $ y $ dato $ x = 0 $ è zero. Non lo sai quasi mai.

$ R ^ 2 $ diventa più alto senza intercettazione, non perché il modello sia migliore, ma perché la definizione di $ R ^ 2 $ usato è un altro! $ R ^ 2 $ è un'espressione di un confronto del modello stimato con un modello standard, espresso come riduzione della somma dei quadrati rispetto alla somma dei quadrati con il modello standard . Nel modello con intercetta, la somma di confronto dei quadrati è intorno alla media. Senza intercettazione, è intorno allo zero! L'ultimo di solito è molto più alto, quindi è più facile ottenere una grande riduzione della somma dei quadrati.

Conclusione: NON LASCIARE L'INTERCETTAZIONE FUORI DAL MODELLO (a meno che tu non sappia veramente cosa stai facendo ).

MODIFICA (dai commenti sotto): un'eccezione è menzionata altrove nei commenti (ma questa è solo apparentemente un'eccezione, il vettore costante 1 si trova nello spazio della colonna della matrice di progettazione $ X $ . Altrimenti, come le relazioni fisiche $ s = vt $ dove non ci sono costanti. Ma anche in questo caso, se il il modello è solo approssimativo (la velocità non è realmente costante), potrebbe essere meglio lasciare una costante anche se non può essere interpretata. Con i modelli non lineari questo diventa più un problema.

1) Non è mai accettabile sopprimere un'intercetta tranne in tipi molto rari di modelli DiD in cui il risultato e i predittori sono effettivamente differenze calcolate tra i gruppi (questo non è il tuo caso).

2). Diamine no, non lo fa. Ciò significa che potresti avere un grado più elevato di validità interna (ad esempio il modello si adatta ai dati) ma probabilmente un basso grado di validità esterna (ad esempio il modello sarebbe scarsa nell'adattamento dei dati sperimentali ottenuti in condizioni simili). Questa è generalmente una cosa negativa.

3) Sopprimere l'intercetta non lo farà necessariamente, ma presumo che il predittore sia stato valutato in modo continuo. In molte situazioni, i tempi di completamento del processo vengono analizzati utilizzando una trasformata inversa, ad es. $ x = 1 / t $ dove $ t $ è il tempo impiegato per completare un processo. L'inverso della media dei dati trasformati inversi è chiamato media armonica e rappresenta il tempo medio di completamento per un'attività.

$$ \ mbox {HM} = \ frac {1} {\ mathbb {E} (x)} = \ frac {1} {\ mathbb {E} (1 / t)} $$

Puoi anche utilizzare un esponenziale parametrico o modelli gamma o weibull time-to-event, che sono tipi di modelli costruiti specificamente per prevedere i tempi di completamento. Questi daranno risultati molto simili ai risultati della trasformazione inversa.

1) È consigliabile forzare l'intercettazione di $ 0 $ se sai per certo che è 0. Qualunque cosa tu sappia a priori , dovresti usarla nel tuo modello.

Uno esempio è il modello di Hubble per l'espansione dell'Universo (usato in Statistical Sleuth ):

$$ \ mbox {Galaxy Speed} = k (\ mbox {Distance from Earth}) $$

Questo modello è piuttosto grezzo, ma utilizza l'intercetta 0 come conseguenza della teoria del Big Bang: al tempo $ 0 $ tutta la questione è in un posto.

Dall'altro il modello che stai descrivendo richiederà probabilmente un termine di intercettazione.

2) Potresti o meno migliorare $ R ^ 2_ {adj} $, oppure potresti accettare ipotesi nulla per il test per l'intercept è 0, ma entrambi non sono motivi per rimuovere il termine di intercettazione.

3) Per garantire la positività delle risposte, a volte puoi trasformare la variabile di risposta. Log o sqrt potrebbero funzionare a seconda dei tuoi dati, ovviamente dovrai controllare i residui.

Ha senso (in realtà, è necessario) omettere l'intercetta nella seconda fase del test di cointegrazione Engle / Granger. Il test stima innanzitutto una relazione di cointegrazione candidata tramite una regressione di una variabile dipendente su una costante (più a volte una tendenza) e le altre variabili non stazionarie.

Nella seconda fase, i residui di quella regressione vengono testati per una radice unitaria per verificare se l'errore rappresenta effettivamente una relazione di equilibrio. Poiché la prima fase di regressione contiene una costante, i residui sono medi zero per costruzione. Quindi, il test della radice unitaria della seconda fase non necessita di una costante e infatti, la distribuzione limite per quel test della radice unitaria viene derivata assumendo che questa costante non sia stata effettivamente adattata.

L'unico modo che conosco per vincolare tutti i valori adattati a essere maggiori di zero è utilizzare un approccio di programmazione lineare e specificarlo come vincolo.

Il vero problema è che una regressione lineare che forza l'intercetta = 0 è un'incongruenza matematica che non dovrebbe mai essere eseguita:

È chiaro che se y = a + bx, allora media (y) = a + media (x), e in effetti possiamo facilmente renderci conto che quando stimiamo aeb usando la stima lineare in Excel, otteniamo la relazione sopra

Tuttavia, se facciamo arbitrariamente a = 0, allora necessariamente b = media (y) / media (x). Ma questo non è coerente con l'algoritmo dei minimi quadrati. In effetti, puoi facilmente capire che quando stimi b usando la stima lineare in Excel, la relazione di cui sopra non è soddisfatta

Ha praticamente senso nei modelli con covariata categoriale. In questo caso la rimozione dell'intercetta produce un modello equivalente con una parametrizzazione solo diversa:

  > data (mtcars) > mtcars $ cyl_factor <- as.factor (mtcars $ cyl) > summary ( lm (mpg ~ cyl_factor, data = mtcars)) Chiamata: lm (formula = mpg ~ cyl_factor, data = mtcars) Residui: Min 1Q Mediana 3Q Max -5.2636 -1.8357 0.0286 1.3893 7.2364 Coefficienti: Std. Errore valore t Pr (> | t |) (Intercept) 26.6636 0.9718 27.437 < 2e-16 *** cyl_factor6 -6.9208 1.5583 -4.441 0.000119 *** cyl_factor8 -11.5636 1.2986 -8.905 8.57e-10 *** --- Signif . codici: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 Errore standard residuo: 3,223 su 29 gradi di libertà R quadrato multiplo: 0,7325 R quadrato rettificato: 0,714 Statistica F: 39.7 su 2 e 29 DF, valore p: 4.979e-09 Riepilogo > (lm (mpg ~ 0 + cyl_factor, data = mtcars)) Call: lm (formula = mpg ~ 0 + cyl_factor, data = mtcars) Residui: Min 1Q Mediana 3Q Max -5,2636 -1,8357 0,0286 1,3893 7,2364 Coefficienti: Std. Errore valore t Pr (> | t |) cyl_factor4 26.6636 0.9718 27.44 < 2e-16 *** cyl_factor6 19.7429 1.2182 16.21 4.49e-16 *** cyl_factor8 15.1000 0.8614 17.53 < 2e-16 *** --- Signif. codici: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 Errore standard residuo: 3,223 su 29 gradi di libertà R quadrato multiplo: 0,9785, R quadrato aggiustato: 0,9763 Statistica F: 440.9 su 3 e 29 DF, valore p: < 2.2e-16  

Il secondo esempio infatti fa sì che la variabile categoriale sia un'intercetta specifica della categoria, quindi in realtà l'intercetta non è effettivamente rimosso, sembra proprio così.