Ho trovato interessante la risposta di BruceET, relativa al numero di eventi. Un modo alternativo per affrontare questo problema è utilizzare la corrispondenza tra tempo di attesa e numero di eventi. L'uso di questo sarebbe che il problema potrà essere generalizzato in qualche modo più facilmente.
Visualizzazione del problema come un problema di tempo di attesa
Questa corrispondenza, come ad esempio spiegata / utilizzata qui e qui, è
Per il numero di tiri dei dadi $ m $ e il numero di risultati / eventi $ k $ tu ottenere:
$$ \ begin {array} {ccc}
\ overbrace {P (K \ geq k | m)} ^ {\ text {questo è quello che stai cercando}} & = &
\ overbrace {P (M \ leq m | k)} ^ {\ text {lo esprimeremo invece}} \\
{\ small \ text {$ \ mathbb {P} $ $ k $ o più eventi in $ m $ rotoli di dadi}} & = & {\ small \ text {$ \ mathbb {P} $ rotoli di dadi inferiori a $ m $ dati $ k $ events}}
\ end {array}
$$
In parole: la probabilità di ottenere più di $ K \ geq k $ eventi (ad es. $ \ geq 1 $ volte 6) in più tiri di dadi $ m $ è uguale alla probabilità di aver bisogno di $ m $ o meno tiri di dado per ottenere $ k $ tali eventi.
Questo approccio riguarda molte distribuzioni.
Distribuzione della distribuzione di
Tempo di attesa tra gli eventi numero di eventi
Poisson esponenziale
Erlang / Gamma di Poisson sovra / sottodisperso
Binomiale geometrico
Binomiale negativo binomiale sovra / sottodisperso
Quindi nella nostra situazione il tempo di attesa è una distribuzione geometrica. La probabilità che il numero di tiri di dadi $ M $ prima di tirare il primo $ n $ è inferiore a o uguale a $ m $ (e data una probabilità di ottenere $ n $ è uguale a $ 1 / n $ ) è il seguente CDF per la distribuzione geometrica:
$$ P (M \ leq m) = 1- \ left (1- \ frac {1} {n} \ right) ^ m $$
e stiamo cercando la situazione $ m = n $ in modo da ottenere:
$$ P (\ text {ci sarà un $ n $ rotolato all'interno di $ n $ rotoli}) = P (M \ leq n) = 1- \ left (1 - \ frac {1} {n} \ right) ^ n $$
Generalizzazioni, quando $ n \ to \ infty $
La prima generalizzazione è che per $ n \ to \ infty $ la distribuzione del numero di eventi diventa Poisson con il fattore $ \ lambda $ e il tempo di attesa diventa una distribuzione esponenziale con il fattore $ \ lambda $ . Quindi il tempo di attesa per lanciare un evento nel processo di lancio dei dadi di Poisson diventa $ (1-e ^ {- \ lambda \ times t}) $ e con $ t = 1 $ otteniamo lo stesso risultato $ \ approx 0.632 $ delle altre risposte. Questa generalizzazione non è ancora così speciale in quanto riproduce solo gli altri risultati, ma per la prossima non vedo così direttamente come potrebbe funzionare la generalizzazione senza pensare ai tempi di attesa.
Generalizzazioni, quando i dadi non sono giusti
Potresti considerare la situazione in cui i dadi non sono giusti. Ad esempio, una volta tirerai con un dado che ha 0,17 probabilità di tirare un 6, e un'altra volta tirerai un dado con 0,16 probabilità di tirare un 6. Ciò significa che i 6 saranno più raggruppati attorno ai dadi con polarizzazione positiva e che la probabilità di ottenere un 6 in 6 turni sarà inferiore alla cifra $ 1-1 / e $ . (significa che in base alla probabilità media di un singolo lancio, diciamo che l'hai determinata da un campione di molti lanci, non puoi determinare la probabilità in molti lanci con lo stesso dado, perché devi tenere conto della correlazione del dadi)
Quindi supponiamo che un dado non abbia una probabilità costante $ p = 1 / n $ , ma invece è tratto da una distribuzione beta con una media $ \ bar {p} = 1 / n $ e alcuni parametri di forma $ \ nu $
$$ p \ sim Beta \ left (\ alpha = \ nu \ frac {1} {n}, \ beta = \ nu \ frac {n-1} {n } \ right) $$
Quindi il numero di eventi per un particolare dado tirato $ n $ tempo sarà binomiale beta distribuito. E la probabilità per 1 o più eventi sarà:
$$ P (k \ geq 1) = 1 - \ frac {B (\ alpha, n + \ beta)} {B (\ alpha, \ beta)} = 1 - \ frac {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} {B (\ nu \ frac {1} {n}, n + \ nu \ frac {n-1} {n})} $$
Posso verificare computazionalmente che funziona ...
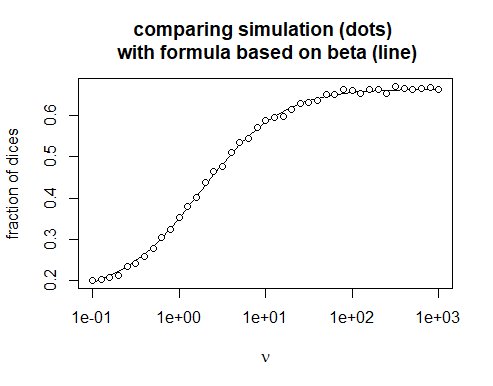
### calcola il risultato per il lancio di dadi a n facce n volte
rolldice <- funzione (n, nu) {
p <- rbeta (1, nu * 1 / n, nu * (n-1) / n)
k <- rbinom (1, n, p)
fuori <- (k>0)
su
}
### calcola la media per un campione di dadi
meandice <- funzione (n, nu, reps = 10 ^ 4) {
sum (replicate (reps, rolldice (n, nu))) / reps
}
meandice <- Vectorize ((meandice))
### simula e calcola la varianza n
set.seed (1)
n <- 6
nu <- 10 ^ seq (-1,3,0.1)
y <- meandice (n, nu)
grafico (nu, 1-beta (nu * 1 / n, n + nu * (n-1) / n) / beta (nu * 1 / n, nu * (n-1) / n), log = "x ", xlab = espressione (nu), ylab =" frazione di dadi ",
main = "confronto simulazione (punti) \ n con formula basata su beta (linea)", main.cex = 1, tipo = "l")
punti (nu, y, lty = 1, pch = 21, col = "black", bg = "white")
.... Ma non ho un buon modo per risolvere analiticamente l'espressione per $ n \ to \ infty $ .
Con il tempo di attesa Tuttavia, con i tempi di attesa, posso esprimere il limite della distribuzione binomiale beta (che ora è più simile a una distribuzione beta di Poisson) con una varianza del fattore esponenziale dei tempi di attesa.
Quindi invece di $ 1-e ^ {- 1} $ stiamo cercando $$ 1- \ int e ^ {- \ lambda} p (\ lambda) \, \ text {d} \, \ lambda $$ .
Ora quel termine integrale è correlato alla funzione di generazione del momento (con $ t = -1 $ ). Quindi, se $ \ lambda $ è normalmente distribuito con $ \ mu = 1 $ e varianza $ \ sigma ^ 2 $ allora dovremmo usare:
$$ 1-e ^ {- (1- \ sigma ^ 2/2)} \ quad \ text {invece di} \ quad 1-e ^ {- 1} $$
Applicazione
Questi rotoli di dadi sono un modello giocattolo. Molti problemi della vita reale avranno variazioni e situazioni di dadi non completamente eque.
Ad esempio, supponi di voler studiare la probabilità che una persona possa ammalarsi a causa di un virus dato un certo tempo di contatto. Si potrebbero basare i calcoli per questo sulla base di alcuni esperimenti che verificano la probabilità di una trasmissione (ad esempio, qualche lavoro teorico, o alcuni esperimenti di laboratorio che misurano / determinano il numero / la frequenza di trasmissioni in un'intera popolazione per una breve durata), e quindi estrapolare questa trasmissione a un intero mese. Supponi di scoprire che la trasmissione è di 1 trasmissione al mese per persona, quindi potresti concludere che $ 1-1 / e \ circa 0,63 \% $ della popolazione riceverà malato. Tuttavia, questa potrebbe essere una sovrastima perché non tutti potrebbero ammalarsi / trasmettere con la stessa velocità. La percentuale sarà probabilmente inferiore.
Tuttavia, questo è vero solo se la varianza è molto grande. Per questo la distribuzione di $ \ lambda $ deve essere molto distorta. Perché, sebbene l'abbiamo espressa come una distribuzione normale in precedenza, i valori negativi non sono possibili e le distribuzioni senza distribuzioni negative in genere non avranno rapporti elevati $ \ sigma / \ mu $ , a meno che non siano molto distorti. Una situazione con un'inclinazione elevata è modellata di seguito:
Ora usiamo l'MGF per una distribuzione di Bernoulli (il suo esponente), perché abbiamo modellato la distribuzione come $ \ lambda = 0 $ con probabilità $ 1-p $ o $ \ lambda = 1 / p $ con probabilità $ p $ .
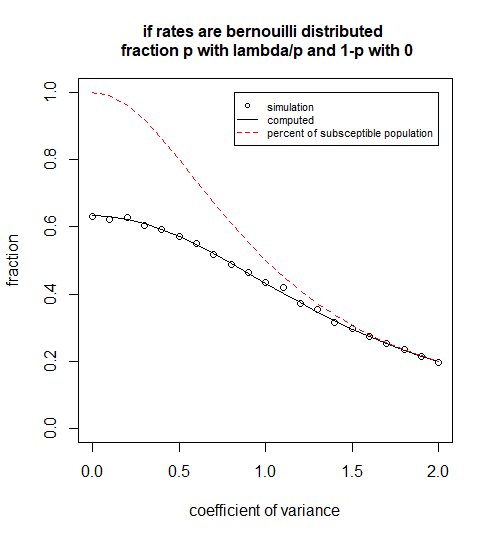
set.seed (1)
tasso = 1
tempo = 1
CV = 1
### calcola il risultato per ammalarti di tasso variabile
getsick <- function (rate, CV = 0.1, time = 1) {
### troncare cambia sd e media ma non molto se CV è piccolo
p <- 1 / (CV ^ 2 + 1)
lambda <- rbinom (1,1, p) / (p) * rate
k <- rpois (1, lambda * time)
fuori <- (k>0)
su
}
CV <- seq (0,2,0.1)
grafico (-1, -1, xlim = c (0,2), ylim = c (0,1), xlab = "coefficiente di varianza", ylab = "frazione",
cex.main = 1, main = "se i tassi sono distribuiti bernouilli \ n frazione p con lambda / pe 1-p con 0")
per (cv in CV) {
punti (cv, sum (replicate (10 ^ 4, getsick (rate = 1, cv, time = 1))) / 10 ^ 4)
}
p <- 1 / (CV ^ 2 + 1)
righe (CV, 1- (1-p) -p * exp (-1 / p), col = 1)
linee (CV, p, col = 2, lty = 2)
legenda (2,1, c ("simulazione", "calcolata", "percentuale di popolazione subsettibile")
col = c (1,1,2), lty = c (NA, 1,2), pch = c (1, NA, NA), xjust = 1, cex = 0,7)
La conseguenza è. Supponi di avere $ n $ elevati e di non avere alcuna possibilità di osservare i tiri dei dadi $ n $ (ad es. a lungo), e invece controlli il numero di $ n $ tiri solo per un breve periodo per molti dadi diversi. Quindi potresti calcolare il numero di dadi che hanno tirato un numero $ n $ durante questo breve periodo e in base a quel calcolo cosa accadrebbe per $ n $ rotola. Ma non sapresti quanto gli eventi sono correlati all'interno dei dadi. Potrebbe essere che tu abbia a che fare con un'alta probabilità in un piccolo gruppo di dadi, invece di una probabilità equamente distribuita tra tutti i dadi.
Questo "errore" (o si potrebbe dire semplificazione) si riferisce alla situazione con COVID-19 in cui l'idea è che abbiamo bisogno del 60% delle persone immuni per raggiungere l'immunità di gregge. Tuttavia, potrebbe non essere così. L'attuale tasso di infezione è determinato solo per un piccolo gruppo di persone, può essere che questa sia solo un'indicazione dell'infezione tra un piccolo gruppo di persone.