Puoi vedere che il tuo argomento non è corretto applicandolo al problema del compleanno standard, dove sappiamo che la probabilità è del 50% a 23 persone. Il tuo argomento restituirà $ \ frac {{23 \ choose 2} {365 \ choose 1}} {365 ^ {23}} $ , che è molto piccolo. Il solito argomento è dire che se vogliamo evitare una coincidenza abbiamo $ 365- (k-1) $ scelte per $ k $ il compleanno della persona, quindi la probabilità di non coincidenza tra $ K $ persone è $ \ prod_ {k = 1} ^ K \ frac {365-k + 1} {365} $

Sfortunatamente, non esiste un argomento così semplice per più di due compleanni coincidenti. C'è solo un modo (fino alla simmetria) per $ k $ persone per non avere coincidenze a due vie, ma ci sono molti, molti modi per non avere quattro vie coincidenza, quindi il calcolo quando si aggiungono persone non è semplice. Ecco perché R fornisce pbirthday () e perché è ancora solo un'approssimazione. Spero certamente che non sia stato un compito in classe.

Il motivo per cui la tua argomentazione non è corretta è che sottostima il numero di modi in cui puoi ottenere 4 mesi corrispondenti. Ad esempio, non è solo che puoi scegliere qualsiasi mese del 12 come quello corrispondente. Puoi anche rietichettare gli altri 11 mesi arbitrariamente (dandoti un fattore di 11!). E il tuo denominatore di $ 12 ^ {18} $ implica che l'ordine delle persone è importante, quindi ci sono più di $ 18 \ scegli 4 ordini $ che hanno 4 corrispondenze.

Sono presenti $ 43 $ partizioni di $ 18 $ in $ 12 $ parti non negative dove la parte più grande è $ 4 $ , mentre ce ne sono un'altra $ 298 $ span> partizioni in cui la parte più grande è maggiore di $ 4 $ e $ 25 $ partizioni in cui la parte più grande è inferiore a $ 4 $ .

Ad esempio una partizione è $$ 18 = 4 + 3 + 3 + 2 + 2 + 1 + 1 + 1 + 1 + 0 + 0 + 0 \\ = 1 \ times 4 + 2 \ volte 3 + 2 \ volte2 + 4 \ volte 1 + 3 \ volte 0 $$

La probabilità che quel particolare schema di partizione si verifichi tra i mesi di nascita della tua squadra è $ \ dfrac {\ dfrac {18!} {4! ^ 1 3! ^ 2 2! ^ 2 1! ^ 4 0! ^ 3} \ times \ dfrac {12!} {1! 2! 2! 4! 3!}} {12 ^ {18}} \ circa 0,05786545 $

Aggiungi le probabilità fino a dove la parte più grande della partizione è $ 4 $ e ottieni circa $ 0,4165314 $ span >; aggiungili dove la parte più grande della partizione è $ 4 $ o più e ottieni circa $ 0,5771871 $ . Queste sono le risposte alla tua domanda.

Nello specifico, le probabilità per le diverse frequenze del mese più frequente sono le seguenti. $ 4 $ risulta essere più probabile e la mediana (la media è di circa $ 3,76 $ )

  Freq della maggior parte dei mesi Probabilità
            1 0
            2 0.0138050
            3 0.4090079
            4 0.4165314
            5 0.1297855
            6 0.0262102
            7 0.0040923
            8 0.0005116
            9 0.0000517
10 0.00000423
           11 0.000000280
           12 0.0000000148
           13 0.000000000622
           14 0.0000000000202
           15 0.000000000000490
           16 0.00000000000000834
           17 0.0000000000000000892
           18 0.000000000000000000451
 

Il modo corretto per risolvere il 2 problema coincidente è calcolare la probabilità che 2 persone non condividano lo stesso mese di compleanno.

In questo esempio, la seconda persona ha una probabilità di 11/12 di non condividere lo stesso mese della prima.
La terza persona ha 10/12 di possibilità di non condividere lo stesso mese con 1 &2.
La quarta persona ha 9/12 di possibilità di non condividere lo stesso mese con 1, 2 & 3.
Quindi la possibilità che nessuno condivida lo stesso mese è $ (11 * 10 * 9) / 12 ^ 3 $ che è circa il 57%. O il 43% di possibilità che almeno 2 condividano lo stesso mese.

Non posso fornire consigli su come estendere questo calcolo manuale al problema 3 o 4 coincidenti. Se conosci R, c'è la funzione pbirthday () per calcolarlo:

  pbirthday (18, classi = 12, coincidente = 4)
[1] 0,5537405
 

Quindi per 18 persone c'è una probabilità del 55% che almeno 4 persone condividano lo stesso mese.

Ecco una buona fonte per comprendere il problema: https://www.math.ucdavis.edu/~tracy/courses/math135A/UsefullCourseMaterial/birthday.pdf

Modifica Per completezza ecco una rapida e sporca simulazione in R:

  quattro <- 0 #count per esattamente 4
fourmore <- 0 #count per 4 o più

count<-100000
for (i in 1: count) {
   #sampiona 12 oggetti, diciotto volte
   m<- campione (1:12, 18, sostituire = TRUE)
   
   if (any (table (m) > = 4)) {fourmore <-fourmore +1}
   if (any (table (m) == 4)) {four <-four +1}
}

stampa (fourmore / count)
# [1] 0,57768
stampa (quattro / conteggio)
# [1] 0.45192
 

Sebbene Henry abbia già fornito un modo per calcolare il numero esattamente contando tutte le partizioni, potrebbe essere interessante conoscere due metodi approssimativi.

Inoltre, esiste un calcolo esatto alternativo basato su variabili distribuite di Poisson condizionali.

Simulazione computazionale

Non sarai facilmente in grado di calcolare tutte le $ 12 ^ {18} $ possibilità (e non sarà facile aumentare il problema), ma puoi fare in modo che un computer simuli in modo casuale un sottoinsieme dei possibili modi e ottenere una distribuzione da quelle simulazioni.

  # funzione per campionare 18 mesi di nascita
# e ottieni il numero massimo di mesi simili
monthsample <- function () {
  x <- sample (1: 12,18, replace = TRUE) # sample
  n <- max (table (x)) # ottiene il massimo
  ritorno (n)
}

# campiona un milione di volte
y <- replicate (10 ^ 6, monthsample ())

# ottiene la frequenza utilizzando un istogramma
h<-hist (y, interruzioni = seq (-0.5,18.5,1))
 

Approssimazione con Poissonation

La frequenza del numero di compleanni in un determinato mese è approssimativamente distribuita Poisson / binomiale. In base a ciò possiamo calcolare la probabilità che il numero di compleanni in un determinato mese non superi un certo valore e, prendendo la potenza di dodici, calcoliamo la probabilità che ciò accada per tutti i dodici mesi.

Nota: qui trascuriamo il fatto che il numero di compleanni è correlato, quindi questo ovviamente non è esatto.

  # approssimazione con distribuzione di Poisson
t <- 0:18
z <- ppois (t, 1.5) ^ 12 # P (max < = t)
dz <- diff (z) # P (max = t + 1)
 

Calcolo con la rappresentazione di Bruce Levin

Nei commenti Whuber ha indicato il pacchetto pmultinom. Questo pacchetto è basato su Bruce Levin 1981 "A Representation for Multinomial Cumulative Distribution Functions" in Ann. Statista. Volume 9 . Il risultato dei mesi di nascita (che è più precisamente distribuito secondo una distribuzione multinomiale) è rappresentato come variabili distribuite di Poisson indipendenti. Ma a differenza del calcolo ingenuo prima menzionato, la distribuzione di quelle variabili distribuite di Poisson è considerata condizionale sul fatto che la somma totale sia uguale a $ n = 18 $ .

Quindi sopra abbiamo calcolato $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4) = P (X_1 \ leq 4) \ cdot P (X_1 \ leq 4) \ cdot \ ldots \ cdot P (X_ {12} \ leq 4) $$ ma avremmo dovuto calcolare la probabilità condizionale che le variabili distribuite di Poisson fossero tutte uguali o inferiori di $$ P (X_1, X_2, \ ldots, X_ {12} \ leq 4 \ vert X_1 + X_2 + \ ldots + X_ {12} = 18) $$ che introduce un termine aggiuntivo basato sulla regola di Bayes.

$$ P (\ forall i: X_i \ leq 4 \ vert \ sum X_i = 18) = P (\ forall i: X_i \ leq 4) \ frac {P ( \ sum X_i = 18 \ vert \ forall i: X_i \ leq 4)} {P (\ sum X_i = 18)} $$

Questo fattore di correzione è il rapporto tra la probabilità che una somma di variabili distribuite di Poisson troncate sia uguale a 18 $ P (\ sum X_i = 18 \ vert \ forall i: X_i \ leq 4 ) $ e la probabilità che una somma di variabili distribuite di Poisson regolari sia uguale a 18, $ P (\ sum X_i = 18) $ . Per una piccola quantità di mesi di nascita e persone nel gruppo questa distribuzione troncata può essere calcolata manualmente

  # fattore di correzione di Bruce Levin
correzione <- function (y) {
  Nptrunc (y) [19] / dpois (18,18)
}

Nptrunc <- function (lim) {

  # distribuzione di Poisson troncata
ptrunc <- dpois (0: lim, 1.5) / sum (dpois (0: lim, 1.5))
  
  ## vettore con probabilità
  outvec <- rep (0, lim * 12 + 1)
  outvec [1] <- 1
  
  #convolve 12 volte per ogni mese
  per (i in 1:12) {
    newvec <- rep (0, lim * 12 + 1)
    for (k in 1: (lim + 1)) {
      newvec <- newvec + ptrunc [k] * c (rep (0, k-1), outvec [1: (lim * 12 + 1- (k-1))])
    }
    outvec <- newvec
  }
  outvec
}

z2 <- ppois (t, 1.5) ^ 12 * Vettorizza (correzione) (t) # P (max< = t)
z2 [1: 2] <- c (0,0)
dz2 <- diff (z2) # P (max = t + 1)
 

Risultati

Queste approssimazioni danno i seguenti risultati

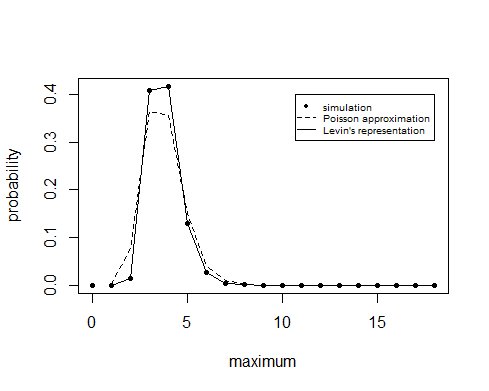
  Simulazione > ###
Somma > (y> = 4) / 10 ^ 6
[1] 0,577536
> ### calcolo
> 1-z [4]
[1] 0,5572514
> ### calcolo esatto
> 1-z2 [4]
[1] 0,5771871
 

È successo che 4 membri del team nel mio gruppo di 18 persone condividessero lo stesso mese di nascita. Diciamo giugno. Quali sono le possibilità che ciò possa accadere? Sto cercando di presentarlo come un problema di probabilità nella riunione del nostro team.

Ci sono molte altre buone risposte qui sulla matematica delle probabilità di calcolo in questi "problemi di compleanno". Un punto da notare è che i compleanni non sono distribuiti uniformemente nei giorni di calendario, quindi l'ipotesi di uniformità utilizzata nella maggior parte delle analisi sottovaluta leggermente la vera probabilità di cluster come questo. Tuttavia, mettendo da parte questo problema, vorrei parlarvi di un po 'di "meta" e incoraggiarvi a pensare a questo problema in modo un po' diverso, poiché implica una grande quantità di "pregiudizi di conferma".

Il bias di conferma si verifica in questo contesto perché è più probabile che tu prenda nota di un risultato e cerchi un'analisi probabilistica di tale risultato se è insolito (cioè, bassa probabilità). Per dirla in un altro modo, pensa a tutte le volte precedenti nella tua vita in cui eri in una stanza con persone e hai imparato il loro mese di compleanno ei risultati non erano insoliti. In quei casi, immagino che non ti sei preso la briga di venire su CV.SE e fare una domanda al riguardo. Quindi il fatto che tu sia qui a porre questa domanda è un importante evento di condizionamento, che accadrebbe solo se osservi qualcosa che è sufficientemente insolito da giustificare la domanda. In considerazione di ciò, la probabilità condizionale del risultato che hai osservato, condizionata dalla tua presenza a porre questa domanda, è piuttosto alta --- molto più alta di quanto suggerirebbe l'analisi nelle altre risposte.

Per esaminare questa situazione in modo più formale, considera questi i seguenti eventi:

$$ \ begin {matrix} \ mathcal {A} (x, y) & & & \ text {Seeing} x \ text {persone con lo stesso mese di compleanno su} y \ text {persone a caso}, \\ [6pt] \ mathcal {B} & & & \ text {Decidere il risultato osservato richiede un'indagine probabilistica}.\ \ end {matrix} $$

La maggior parte delle risposte qui ti dicono come stimare $ \ mathbb {P} (\ mathcal {A} (4,18)) $ ma l'effettivola probabilità in gioco qui è la probabilità condizionale $ \ mathbb {P} (\ mathcal {A} (4,18) | \ mathcal {B}) $ , che èmuch, much superiore (e non può essere calcolato qui).

La matematica è molto al di là di me.Tuttavia, questo genere di cose mi affascina, quindi ho costruito un foglio di calcolo per replicarlo per 10.000 gruppi di 18 persone ciascuno con un mese di nascita generato a caso.Ho quindi contato quanti di questi gruppi avevano esattamente quattro persone con un mese di nascita condiviso.Per i puristi, poiché la domanda non ha specificato, ho incluso anche eventuali incidenze di quattro persone che condividono un mese di nascita e quattro persone separate che condividono un mese di nascita diverso.Inoltre non ho escluso tre o quattro gruppi di quattro che condividono rispettivamente tre o quattro diversi mesi di nascita.

Ho eseguito questo foglio di calcolo 50 volte e il risultato più basso che ho ottenuto è stato del 43,95%.Il più alto è stato del 46,16%.La media era del 45,05%.

Lascerò a qualcuno più esperto di fare i conti per convalidare questo risultato approssimativo!

Questo è un problema con le palle nei contenitori.

La probabilità che l'occupazione massima di qualsiasi contenitore sia $ m $ , data $ n $ binse $ r $ palline allocate casualmente è il coefficiente di $ x ^ r $ in

$ \ begingroup \ Large \ begin {equation} \ left (\ sum _ {i = 0} ^ m \ frac {x ^ i} {i!} \ right)^ n \ end {equation} \ endgroup $

moltiplicato per $ \ begingroup \ Large \ begin {equation} r!n ^ {- r} \ end {equation} \ endgroup $

La valutazione di questo per i casi "4 o più" e "esattamente 4" produce $$ \ frac {555795868793273} {962938848411648} \ circa 0,577187 $$ e $$ \ frac {19807122209875} {47552535724032} \ approx 0.416531 $$ rispettivamente per la tua query.