Normalmente non chiameresti il ​​valore osservato un "valore stimato".

Tuttavia, nonostante ciò, il valore osservato è nondimeno tecnicamente una stima della media al suo particolare $ x $, e trattarlo come una stima ci dirà effettivamente senso in cui OLS è più bravo a stimare la media lì.

In generale, la regressione viene utilizzata nella situazione in cui se si prendesse un altro campione con gli stessi $ x $, non si otterrebbero gli stessi valori per $ y $. Nella regressione ordinaria, trattiamo $ x_i $ come quantità fisse / note e le risposte, $ Y_i $ come variabili casuali (con valori osservati denotati da $ y_i $).

Usando una notazione più comune, scriviamo

$$ Y_i = \ alpha + \ beta x_i + \ varepsilon_i $$

Il termine rumore, $ \ varepsilon_i $, è importante perché le osservazioni non sono corrette sulla linea della popolazione (se lo facessero non ci sarebbe bisogno di regressione; due punti qualsiasi ti darebbero la linea della popolazione); il modello per $ Y $ deve tenere conto dei valori che assume e, in questo caso, la distribuzione dell'errore casuale tiene conto delle deviazioni dalla linea ("vera").

La stima della media al punto $ x_i $ per la regressione lineare ordinaria ha varianza

$$ \ Big (\ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} \ Big) \, \ sigma ^ 2 $$

mentre la stima basata sul valore osservato ha varianza $ \ sigma ^ 2 $.

È possibile mostrare che per $ n $ almeno 3, $ \, \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum (x_i- \ bar {x}) ^ 2} $ non è più di 1 (ma può essere - e in pratica di solito è - molto più piccolo). [Inoltre, quando si stima l'adattamento a $ x_i $ per $ y_i $, rimane anche il problema di come stimare $ \ sigma $.]

Ma invece di perseguire la dimostrazione formale, medita un esempio, che spero possa essere più motivante.

Sia $ v_f = \ frac {1} {n} + \ frac {(x_i- \ bar {x}) ^ 2} {\ sum ( x_i- \ bar {x}) ^ 2} $, il fattore per il quale viene moltiplicata la varianza dell'osservazione per ottenere la varianza dell'adattamento a $ x_i $.

Tuttavia, lavoriamo sulla scala dell'errore standard relativo piuttosto che sulla varianza relativa (cioè, guardiamo la radice quadrata di questa quantità); gli intervalli di confidenza per la media in un particolare $ x_i $ saranno un multiplo di $ \ sqrt {v_f} $.

Quindi per l'esempio. Prendiamo i dati di cars in R; si tratta di 50 osservazioni raccolte negli anni '20 sulla velocità delle auto e sulle distanze prese per fermarsi:

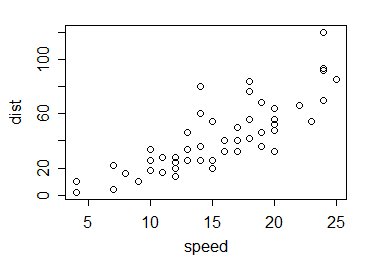
Allora come funzionano i valori di $ \ sqrt {v_f} $ confrontare con 1? In questo modo:

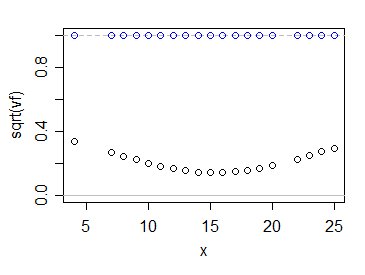
I cerchi blu mostrano i multipli di $ \ sigma $ per la tua stima, mentre quelli neri lo mostrano per la solita stima dei minimi quadrati. Come vedi, l'utilizzo delle informazioni di tutti i dati rende la nostra incertezza su dove si trova la media della popolazione sostanzialmente più piccola, almeno in questo caso, e ovviamente dato che il modello lineare è corretto.

Di conseguenza , se tracciamo (diciamo) un intervallo di confidenza del 95% per la media per ogni valore $ x $ (anche in luoghi diversi da un'osservazione), i limiti dell'intervallo ai vari $ x $ sono tipicamente piccoli rispetto al variazione nei dati:

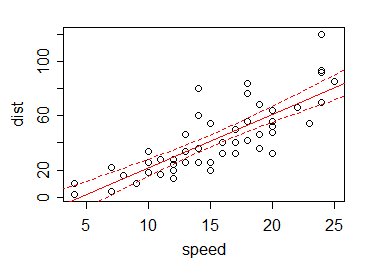
Questo è il vantaggio di "prendere in prestito" informazioni da valori di dati diversi da quello attuale.

In effetti, possiamo utilizzare le informazioni di altri valori - tramite la relazione lineare - per ottenere buone stime del valore in luoghi in cui non abbiamo nemmeno i dati. Considera che nel nostro esempio non ci sono dati a x = 5, 6 o 21. Con lo stimatore suggerito, non abbiamo informazioni lì - ma con la retta di regressione possiamo non solo stimare la media in quei punti (e in 5,5 e 12,8 e così via), possiamo fornire un intervallo, anche se, ancora una volta, uno che si basa sull'idoneità delle ipotesi di linearità (e varianza costante di $ Y $ s e indipendenza).

Innanzitutto, l'equazione di regressione è:

\ begin {equation} Y_i = \ alpha + \ beta X_i + \ epsilon_i \ end {equation}

È presente un termine di errore , $ \ epsilon $. A quanto pare, questo termine di errore è fondamentale per rispondere alla tua domanda. Qual è esattamente il termine di errore nella tua applicazione? Un'interpretazione comune è "l'influenza di tutto, tranne $ X $, che influisce su $ Y $". Se questa è la tua interpretazione del termine di errore, allora $ Y_i $ è la misura migliore di ciò che è realmente $ Y_i $.

D'altra parte, in alcuni rari casi interpretiamo il termine di errore come se fosse esclusivamente errore di misura --- l'errore indotto dall'errore dell'operatore nell'uso di uno strumento scientifico o l'errore derivante dalla precisione naturalmente limitata di uno strumento. In tal caso, il valore "reale" di $ Y_i $ è $ \ alpha + \ beta X_i $. In questo caso, dovresti usare la previsione OLS di $ Y_i $ invece del valore effettivo di $ Y_i $ se $ V (\ epsilon_i) >V (\ hat {\ alpha} _ {OLS} + \ hat {\ beta} _ {OLS} X_i) $ --- cioè se la varianza dell'errore derivante dalla sostituzione di $ \ alpha $ e $ \ beta $ con i loro stimatori OLS è minore della varianza dell'errore di misurazione.

Il valore originale non è una stima (tranne per il fatto che potrebbe avere un errore di misurazione): è il valore di Y per un soggetto specifico (ad es. persona o qualsiasi altra cosa). Il valore previsto dall'equazione è una stima: è una stima del valore atteso di Y a un dato valore di X.

Rendiamolo concreto:

Supponiamo che Y sia peso e X è l'altezza. Diciamo che misuri e pesi un gruppo di persone. Diciamo che Jill è 5'0 e 105 libbre. Questa è la sua altezza e il suo peso. L'equazione ti darà un valore di peso previsto diverso per una persona che è 5'0 ". Questo non è il valore previsto per Jill: non è necessario prevedere o stimare il suo peso, lo sai con la precisione del scala È il valore previsto di una "persona tipica 5'0".

L'equazione dovrebbe essere $$ \ operatorname {E} (Y) = \ alpha + \ beta x $$; questo è il valore atteso di $ Y $ al valore dato di $ x $. Quindi, se il tuo modello ha & corretto, fai abbastanza osservazioni di $ Y $ a quel valore di $ x $, ti dice quale sarà il valore medio di $ Y $. A lungo termine farai meglio a fare previsioni utilizzando quella media rispetto al valore che hai osservato.

Tipicamente, OLS non è tipicamente motivato dal confronto tra la risposta stimata, $ \ hat {Y_i} $, alla risposta osservata $ Y_i $. Se invece viene fornito un nuovo insieme di valori per il valore predittore $ X_ {new} $, il modello OLS prevede quale sarebbe la variabile dipendente $ \ hat {Y} _ {new} $ in un caso tipico.

Il punto è che $ \ hat {Y} _i $ in genere non è considerato "migliore" di $ Y_i $, ma piuttosto un riflesso più accurato di ciò che ti aspetti che $ Y $ sia a un valore particolare per $ X $ .

Tuttavia, ci sono situazioni in cui potresti pensare che $ \ hat {Y} _i $ rifletta la verità in modo più accurato di $ Y_i $ (forse per un valore anomalo derivante da un malfunzionamento nella tua raccolta di dati). Ciò dipenderà fortemente dai dettagli dei tuoi dati.

Questo aiuta? (Era ciò che mi è venuto in mente per la prima volta leggendo la domanda.)

In statistica, il teorema di Gauss-Markov, dal nome di Carl Friedrich Gauss e Andrey Markov, afferma che in un modello di regressione lineare in cui gli errori hanno aspettativa zero e non sono correlati e hanno varianze uguali, il miglior stimatore lineare corretto (BLU) dei coefficienti è dato dallo stimatore dei minimi quadrati ordinari (OLS). In questo caso "migliore" significa fornire la varianza più bassa della stima, rispetto ad altre stime lineari e imparziali. Non è necessario che gli errori siano normali, né indipendenti e distribuiti in modo identico (solo non correlati e omoschedastici). L'ipotesi che lo stimatore sia corretto non può essere abbandonata, poiché altrimenti esistono stimatori migliori di OLS.

http://en.wikipedia.org/wiki/Gauss%E2%80%93Markov_theorem